题目内容
与直线4x-3y+1=0平行且距离为2的直线方程为 ．
【答案】分析：设所求的直线方程为 4x-3y+c=0，根据与直线4x-3y+1=0的距离为2 得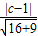
=2，解得c值，即得所求的直线方程．
解答：解：设所求的直线方程为4x-3y+c=0，根据与直线4x-3y+1=0的距离为2得
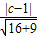=2，解得c=11，或 c=-9，故所求的直线方程为4x-3y+11=0或4x-3y-9=0．
故答案为4x-3y+11=0或4x-3y-9=0．
点评：题考查两直线平行的性质，两平行线间的距离公式，设出所求的直线方程为 4x-3y+c=0，是解题的突破口．
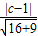=2，解得c值，即得所求的直线方程．解答：解：设所求的直线方程为4x-3y+c=0，根据与直线4x-3y+1=0的距离为2得
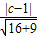=2，解得c=11，或 c=-9，故所求的直线方程为4x-3y+11=0或4x-3y-9=0．故答案为4x-3y+11=0或4x-3y-9=0．
点评：题考查两直线平行的性质，两平行线间的距离公式，设出所求的直线方程为 4x-3y+c=0，是解题的突破口．
练习册系列答案
相关题目
与直线4x+3y + 1 ＝0相切，动圆M与
及y轴都相切. (I )求点M的轨迹C的方程；(II)过点F任作直线l，交曲线C于A，B两点，由点A，B分别向
各引一条切线，切点 分别为P，Q，记
.求证
是定值.