题目内容
(本小题满分12分)
已知点F( 1,0), 与直线4x+3y + 1 =0相切,动圆M与
与直线4x+3y + 1 =0相切,动圆M与 及y轴都相切. (I )求点M的轨迹C的方程;(II)过点F任作直线l,交曲线C于A,B两点,由点A,B分别向
及y轴都相切. (I )求点M的轨迹C的方程;(II)过点F任作直线l,交曲线C于A,B两点,由点A,B分别向 各引一条切线,切点 分别为P,Q,记
各引一条切线,切点 分别为P,Q,记 .求证
.求证 是定值.
是定值.
【答案】
(I )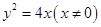 ;(II) 当不与
;(II) 当不与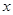 轴垂直时,直线的方程为
轴垂直时,直线的方程为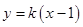 ,由
,由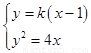 得
得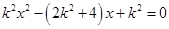 ,设
,设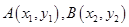 ,
,
∴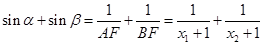
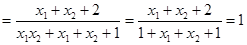 ,
,
当与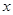 轴垂直时,也可得
轴垂直时,也可得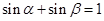 。
。
【解析】
试题分析:(Ⅰ)⊙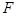 的半径为
的半径为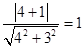 ,⊙
,⊙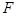 的方程为
的方程为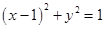 ,
,
作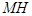 ⊥
⊥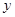 轴于
轴于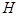 ,则
,则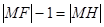 ,即
,即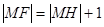 ,则
,则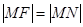 (
(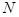 是过
是过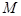 作直线
作直线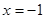 的垂线的垂足),则点
的垂线的垂足),则点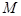 的轨迹是以
的轨迹是以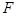 为焦点,
为焦点,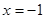 为准线的抛物线.
为准线的抛物线.
∴点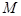 的轨迹
的轨迹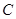 的方程为
的方程为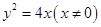 ;
…6分
;
…6分
(Ⅱ)当不与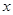 轴垂直时,直线的方程为
轴垂直时,直线的方程为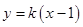 ,由
,由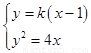 得
得
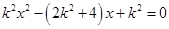 ,设
,设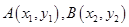 ,则
,则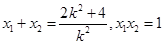
∴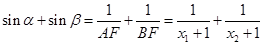
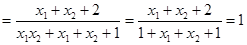 ,
,
当与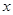 轴垂直时,也可得
轴垂直时,也可得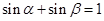 ,
,
综上,有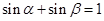 .
…12分
.
…12分
考点:轨迹方程的求法;抛物线的简单性质;直线方程的点斜式;直线与抛物线的综合应用。
点评:(1)在设直线方程的点斜式时,要注意讨论斜率是否存在;(2)做第二问的关键是:把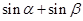 的值用两根之和或两根之积表述出,从而达到应用韦达定理的目的。
的值用两根之和或两根之积表述出,从而达到应用韦达定理的目的。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目