题目内容
1.已知复数z=$\frac{5}{1-2i}$,则复数z的共轭复数所在的象限是( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 直接由复数代数形式的乘除运算化简复数z,得到复数z的共轭复数,然后求出在复平面内对应的点的坐标,则答案可求.
解答 解:∵z=$\frac{5}{1-2i}$=$\frac{5(1+2i)}{(1-2i)(1+2i)}=1+2i$,
∴复数z的共轭复数为:1-2i,在复平面内对应的点的坐标为:(1,-2),位于第四象限.
故选:D.
点评 本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
16.在平行四边形ABCD中,AB=2,AD=1,∠BAD=60°,E为线段CD上一动点,则$\overrightarrow{AE}•\overrightarrow{BD}$的取值范围是[-3,0].
6.执行如图的程序框图,若输入的x的值为1,则输出的y的值是( )


| A. | 1 | B. | 4 | C. | 7 | D. | 13 |
13.已知两个命题:
p:“若复数z1,z2满足z1-z2>0,则z1>z2.”;
q:“存在唯一的一个实数对(a,b)使得a-bi=i(2+i).”
其真假情况是( )
p:“若复数z1,z2满足z1-z2>0,则z1>z2.”;
q:“存在唯一的一个实数对(a,b)使得a-bi=i(2+i).”
其真假情况是( )
| A. | p真q假 | B. | p假q假 | C. | p假q真 | D. | p真q真 |
10.sin$\frac{17π}{3}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
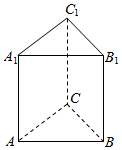 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=AC=2,AA1=4
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=AC=2,AA1=4