题目内容
4．函数f（x）=lnx+ax有大于1的极值点，则a的取值范围是（-1，0）．分析 先对函数进行求导令导函数等于0，原函数有大于1的极值点，故导函数有大于1的根．
解答 解：∵y=lnx+ax，
∴y′=$\frac{1}{x}$+a，
由y′=0，得x=-$\frac{1}{a}$，
∵x＞1，∴$-\frac{1}{a}＞1$
即$\frac{a+1}{a}＜0$，解得-1＜a＜0
∴a的取值范围为（-1，0）．
故答案为：（-1，0）
点评 本题主要考查函数的极值与其导函数的关系，求解过程中要注意导数性质的合理运用．属于基础题型．
练习册系列答案
相关题目
12．若不等式组$\left\{\begin{array}{l}x-y+2≥0\\ x-5y+10≤0\\ x+y-8≤0\end{array}\right.$所表示的平面区域存在点（x0，y0）使x0+ay0+2≤0成立，则实数a的取值范围是（ ）
| A． | a＞1 | B． | a＞-1 | C． | a≤1 | D． | a≤-1 |
19．下列四个函数中，既是奇函数又是定义域上的单调递增的是（ ）
| A． | y=2-x | B． | y=tanx | C． | y=x3 | D． | y=log3x |
9．设函数f（x）=2x3+3ax2+3bx+8c在x=1及x=2时取得极值，若对于任意的x∈[0，3]，都有f（x）＜c2成立，则实数c的取值范围为（ ）
| A． | （-1，9） | B． | （-9，1） | C． | （-∞，-1）∪（9，+∞） | D． | （-∞，-9）∪（1，+∞） |
13．
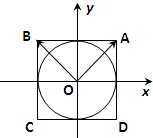如图，在平面直角坐标系xoy中，圆x2+y2=r2（r＞0）内切于正方形ABCD，任取圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则$\frac{1}{4}$是m2，n2的等差中项，现有一椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）内切于矩形ABCD，任取椭圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则m2，n2的等差中项为（ ）
如图，在平面直角坐标系xoy中，圆x2+y2=r2（r＞0）内切于正方形ABCD，任取圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则$\frac{1}{4}$是m2，n2的等差中项，现有一椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）内切于矩形ABCD，任取椭圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则m2，n2的等差中项为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | 1 |
11．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1，（$\overrightarrow{a}$+2$\overrightarrow{b}$）•（$\overrightarrow{a}$-$\overrightarrow{b}$）=-$\frac{1}{2}$，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |