题目内容
9.设函数f(x)=2x3+3ax2+3bx+8c在x=1及x=2时取得极值,若对于任意的x∈[0,3],都有f(x)<c2成立,则实数c的取值范围为( )| A. | (-1,9) | B. | (-9,1) | C. | (-∞,-1)∪(9,+∞) | D. | (-∞,-9)∪(1,+∞) |
分析 根据条件得f′(1)=0,f′(2)=0.求解即可求出a,b的值,若对任意的x∈[0,3],都有f(x)<c2成立?f(x)max<c2在区间[0,3]上成立,根据导数求出函数在[0,3]上的最大值,进一步求c的取值范围.
解答 解:函数的f(x)的导数f′(x)=6x2+6ax+3b,
∵函数f(x)在x=1及x=2取得极值,则有f′(1)=0,f′(2)=0.
即$\left\{\begin{array}{l}{6+6a+3b=0}\\{24+12a+3b=0}\end{array}\right.$,
解得a=-3,b=4.
即f(x)=2x3-9x2+12x+8c,f′(x)=6x2-18x+12=6(x-1)(x-2).
由f′(x)>0得0<x<1或2<x<3;
由f′(x)<0得1<x<2.
故当x=1时,f(x)取得极大值f(1)=5+8c,又f(0)=8c,f(3)=9+8c.
则当x∈[0,3]时,f(x)的最大值为f(3)=9+8c.
∵对于任意的x∈[0,3],有f(x)<c2恒成立,
∴9+8c<c2,
解得c<-1或c>9,
因此c的取值范围为(-∞,-1)∪(9,+∞).
故选:C
点评 本题考查导数的运用:求单调区间和极值、最值,同时考查不等式恒成立问题转化为求函数的最值问题,属于中档题和易错题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.知a1=1,an+1=$\frac{a_n}{{3{a_n}+1}}$,则数列{an}的通项为an=( )
| A. | $\frac{1}{2n-1}$ | B. | 2n-1 | C. | $\frac{1}{3n-2}$ | D. | 3n-2 |
17.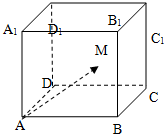 如图,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率是( )
如图,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率是( )
 如图,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率是( )
如图,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率是( )| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
16.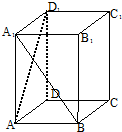 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |