Question

13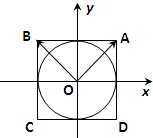．如图，在平面直角坐标系xoy中，圆x²+y²=r²（r＞0）内切于正方形ABCD，任取圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则$\frac{1}{4}$是m²，n²的等差中项，现有一椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）内切于矩形ABCD，任取椭圆上一点P，若$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则m²，n²的等差中项为（　　）

• A． $\frac{1}{4}$
• B． $\frac{1}{2}$
• C． $\frac{\sqrt{2}}{2}$
• D． 1

Answer 1

分析 设出P的坐标，由$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$把P的坐标用含有m，n的代数式表示，代入椭圆方程得答案．

解答 解：设P（x，y），则
由题意，$\overrightarrow{OA}$=（a，b），$\overrightarrow{OB}$=（-a，b），
∵$\overrightarrow{OP}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$，
∴（x，y）=（ma，mb）+（-na，nb），
∴x=（m-n）a，y=（m+n）b，
∴$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=$\frac{（m-n）^{2}{a}^{2}}{{a}^{2}}+\frac{（m+n）^{2}{b}^{2}}{{b}^{2}}=1$，
即${m}^{2}+{n}^{2}=\frac{1}{2}$．
故选：B．

点评 本题是新定义题，考查了平面向量的坐标运算，是基础题．