题目内容
已知数列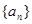 满足
满足 ,
,
(1)证明:数列 是等比数列,并求出
是等比数列,并求出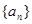 的通项公式
的通项公式
(2)设数列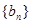 的前n项和为
的前n项和为 ,且对任意
,且对任意 ,有
,有 成
成
立,求
(1) (2)
(2)
解析试题分析:(1)由 可得
可得 ,
, 是以2为首项,3为公比的等比数列
是以2为首项,3为公比的等比数列

(2) 时,
时,
 时,
时,


设
则


综上,
考点:等比数列 求和公式综合运用
点评:本题主要考查了数列的通项公式和数列的求和,考查了学生的计算能力和对数列的综
合掌握,解题时注意整体思想和转化思想的运用,属于中档题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
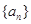 的所有项均为正数,首项
的所有项均为正数,首项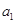 =1,且
=1,且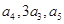 成等差数列.
成等差数列.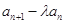 }的前
}的前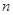 项和为
项和为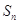 ,若
,若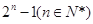 ,求实数
,求实数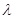 的值.
的值.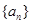 中,
中,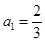 ,且对任意的
,且对任意的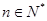 都有
都有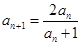 .
.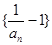 是等比数列;
是等比数列;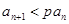 ,求实数
,求实数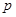 的取值范围.
的取值范围. 是等比数列
是等比数列 的前
的前 项和,且
项和,且 ,
, .
. ;
; ,求数列
,求数列 的前
的前 .
. }中
}中
 ,求证数列{
,求证数列{ }是等比数列;
}是等比数列; }的前n 项和为
}的前n 项和为 ,已知
,已知 ,
, ,
, 成等差数列
成等差数列 ;
; -
- =3,求
=3,求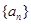 中,
中,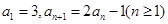
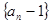 是等比数列;
是等比数列; ,求证:数列
,求证:数列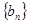 的前
的前 项和
项和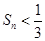 .
.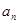 与
与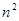 的大小(
的大小( )。
)。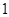 和
和 之间插入
之间插入 个实数,使得这
个实数,使得这 个数构成递增的等比数列,将这
个数构成递增的等比数列,将这 ,令
,令 ,
, N
N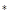 .
.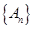 的前
的前 ;
; .
.