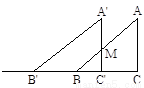题目内容
Rt△ABC中,斜边BC为m,以BC的中点O为圆心作直径为n (n<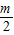 )的圆,分别交BC于P,Q两点,求|AP|2+|AQ|2+|PQ|2的值.
)的圆,分别交BC于P,Q两点,求|AP|2+|AQ|2+|PQ|2的值.
【答案】分析:利用余弦定理,求出|AP|2、|AQ|2,结合∠AOP+∠AOQ=180°,即可求|AP|2+|AQ|2+|PQ|2的值.
解答:解:由题意,OA=OB=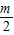 ,OP=OQ=n
,OP=OQ=n
△AOP中,根据余弦定理AP2=OA2+OP2-2OA•OPcos∠AOP
同理△AOQ中,AQ2=OA2+OQ2-2OA•OQcos∠AOQ
因为∠AOP+∠AOQ=180°,
所以|AP|2+|AQ|2+|PQ|2=2OA2+2OP2+PQ2=2(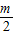 )2+2n2+(2n)2=
)2+2n2+(2n)2=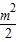 +6n2.
+6n2.
点评:本题考查直线与圆的位置关系,考查余弦定理的运用,考查学生的计算能力,属于基础题.
解答:解:由题意,OA=OB=
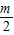 ,OP=OQ=n
,OP=OQ=n△AOP中,根据余弦定理AP2=OA2+OP2-2OA•OPcos∠AOP
同理△AOQ中,AQ2=OA2+OQ2-2OA•OQcos∠AOQ
因为∠AOP+∠AOQ=180°,
所以|AP|2+|AQ|2+|PQ|2=2OA2+2OP2+PQ2=2(
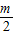 )2+2n2+(2n)2=
)2+2n2+(2n)2=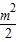 +6n2.
+6n2.点评:本题考查直线与圆的位置关系,考查余弦定理的运用,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
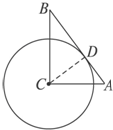 (2013•肇庆二模)(几何证明选讲选做题)
(2013•肇庆二模)(几何证明选讲选做题)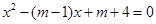 的两根,
的两根,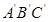 与△ABC开始时完全重合,然后让△ABC固定不动,将
与△ABC开始时完全重合,然后让△ABC固定不动,将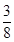 平方厘米?
平方厘米?