题目内容
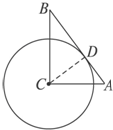（2013•肇庆二模）（几何证明选讲选做题）如图，在Rt△ABC中，斜边AB=12，直角边AC=6，如果以C为圆心的圆与AB相切于D，则⊙C的半径长为
3
| 3 |
3
．| 3 |
分析：在Rt△ABC中，利用勾股定理即可得出BC．又AB与⊙C相切与点D，连接CD，得到CD⊥AB．利用S△ABC=
AC•BC=
AB•CD，即可得出⊙C的半径CD．
| 1 |
| 2 |
| 1 |
| 2 |
解答：解：在在Rt△ABC中，斜边AB=12，直角边AC=6，∴BC=
=
=6
．
∵AB与⊙C相切与点D，连接CD，∴CD⊥AB．
∴S△ABC=
AC•BC=
AB•CD，∴CD=
=
=3
．
∴⊙C的半径长为3
．
故答案为3
．
| AB2-AC2 |
| 122-62 |
| 3 |
∵AB与⊙C相切与点D，连接CD，∴CD⊥AB．
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| AC•BC |
| AB |
6×6
| ||
| 12 |
| 3 |
∴⊙C的半径长为3
| 3 |
故答案为3
| 3 |
点评：熟练掌握勾股定理、圆的切线的性质和“等面积变形”是解题的关键．
练习册系列答案
相关题目