题目内容
据统计某种汽车的最高车速为120千米∕时,在匀速行驶时每小时的耗油量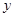 (升)与行驶速度
(升)与行驶速度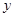 (千米∕时)之间有如下函数关系:
(千米∕时)之间有如下函数关系: 。已知甲、乙两地相距100千米。
。已知甲、乙两地相距100千米。
(1)若汽车以40千米∕时的速度匀速行驶,则从甲地到乙地需耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
(1)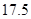 ,(2)当汽车以
,(2)当汽车以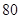 千米∕时的速度行驶时,从甲地到乙地耗油最少,最少为
千米∕时的速度行驶时,从甲地到乙地耗油最少,最少为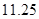 升
升
解析试题分析:(1)解实际问题应用题,需正确理解题目含义. 从甲地到乙地需耗油等于每小时的耗油量乘以行驶时间. 从甲地到乙地行驶了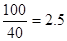 (小时),每小时的耗油量为,
(小时),每小时的耗油量为,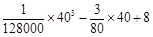 ,所以共需耗油
,所以共需耗油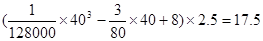 ,(2)在(1)的基础上,将从甲地到乙地耗油表示为速度的函数关系式:
,(2)在(1)的基础上,将从甲地到乙地耗油表示为速度的函数关系式: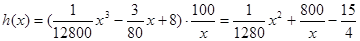 ,利用导数求出其极小值,也是最小值.解题过程中需明确极值点是否在定义区间内.
,利用导数求出其极小值,也是最小值.解题过程中需明确极值点是否在定义区间内.
试题解析:解:(1)当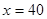 时,汽车从甲地到乙地行驶了
时,汽车从甲地到乙地行驶了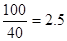 (小时),
(小时),
需耗油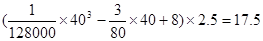 (升)。
(升)。
所以汽车以40千米∕时的速度匀速行驶,从甲地到乙地需耗油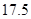 升 …4分.
升 …4分.
(2)当汽车的行驶速度为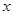 千米∕时时,从甲地到乙地需行驶
千米∕时时,从甲地到乙地需行驶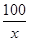 小时.
小时.
设耗油量为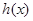 升,依题意,得
升,依题意,得 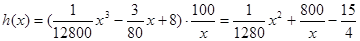 ,
,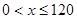 .……7分
.……7分
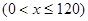 .
.
令 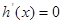 ,得
,得 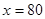 .
.
因为当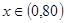 时,
时,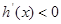 ,
,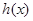 是减函数;当
是减函数;当 时,
时,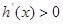 ,
,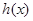 是增函数,所以当
是增函数,所以当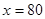 时,
时,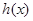 取得最小值
取得最小值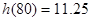 .
.
所以当汽车以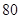 千米∕时的速度行驶时,从甲地到乙地耗油最少,
千米∕时的速度行驶时,从甲地到乙地耗油最少,
最少为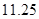 升。 12分
升。 12分
考点:利用导数求实际问题最值

练习册系列答案
相关题目
 -(2+a)lnx(a≥0).
-(2+a)lnx(a≥0).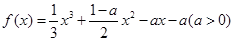 .
.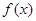 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;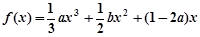 ,
,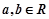 ,
,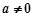 ,
, 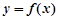 与
与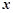 轴相切于异于原点的一点,且函数
轴相切于异于原点的一点,且函数 的极小值为
的极小值为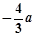 ,求
,求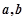 的值;
的值;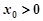 ,且
,且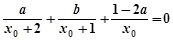 ,
,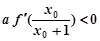 ; ②求证:
; ②求证: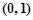 上存在极值点.
上存在极值点. .
. 的最小值;
的最小值;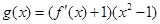 ,试问函数
,试问函数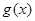 在
在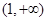 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由. ,关于x的不等式
,关于x的不等式 的解集为
的解集为 ,其中m为非零常数.设
,其中m为非零常数.设 .
. 如何取值时,函数
如何取值时,函数 存在极值点,并求出极值点;
存在极值点,并求出极值点;
 ax2-(2a+1)x+2lnx(a∈R).
ax2-(2a+1)x+2lnx(a∈R).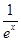 -
-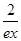 成立.
成立.