题目内容
设函数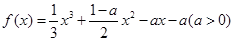 .
.
(1)若函数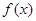 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;
(2)当a=1时,求函数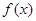 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.
(1)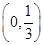 (2)
(2)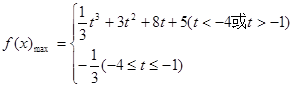
解析试题分析:
(1)根据题意对函数 求导,获得导函数
求导,获得导函数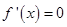 的根与大于0小于0的解集,获得函数
的根与大于0小于0的解集,获得函数 的单调区间和极值点,极值.进而确定函数
的单调区间和极值点,极值.进而确定函数 在区间
在区间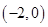 上的单调性,再利用数形结合的思想与零点存在性定理的知识可以得到函数在
上的单调性,再利用数形结合的思想与零点存在性定理的知识可以得到函数在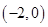 上要有两个零点,需要
上要有两个零点,需要 满足
满足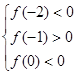 即可,解不等式即可求出
即可,解不等式即可求出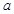 的取值范围.
的取值范围.
(2)根据题意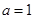 ,则利用(1)可以得到
,则利用(1)可以得到 的单调性以及极值点,极值.要得到函数
的单调性以及极值点,极值.要得到函数 在含参数的区间
在含参数的区间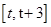 上的最大值,我们需要讨论
上的最大值,我们需要讨论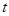 的范围得到函数
的范围得到函数 的在区间
的在区间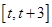 上的单调性进而得到
上的单调性进而得到 在该区间上的最大值,为此分三种情况分别为
在该区间上的最大值,为此分三种情况分别为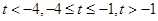 ,依次确定单调性得到最大值即可.
,依次确定单调性得到最大值即可.
试题解析:
(1)∵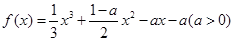
∴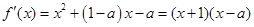 , (1分)
, (1分)
令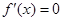 ,解得
,解得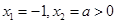 (2分)
(2分)
当x变化时,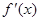 ,
,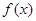 的变化情况如下表:
的变化情况如下表:
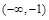
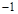


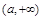
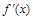
0 — 0 
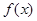
↗ 极大值 ↘ 极小值  练习册系列答案
练习册系列答案
中考对策全程复习方案系列答案
王朝霞中考真题精编系列答案
阅读旗舰文言文课内阅读系列答案
中考一线题系列答案
中考真题超详解系列答案
中考必刷题系列答案
新课程新练习系列答案

名校百分卷系列答案
波波熊语文题卡系列答案
相关题目
 .
. 且
且 时,证明:
时,证明: ;
; ,
, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 时,证明:
时,证明: .
.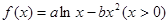 ,若函数
,若函数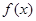 在
在 处与直线
处与直线 相切,
相切,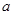 ,
, 的值;(2)求函数
的值;(2)求函数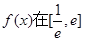 上的最大值.
上的最大值.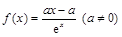
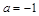 时,求函数
时,求函数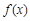 的极值;
的极值;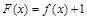 没有零点,求实数a取值范围.
没有零点,求实数a取值范围. ,当
,当 时,
时,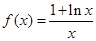 .
.
 上存在极值点,求实数a的取值范围;
上存在极值点,求实数a的取值范围; 时,不等式
时,不等式 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
 .
.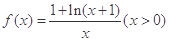
 在区间
在区间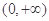 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论;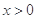 时,
时,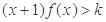 恒成立,求整数
恒成立,求整数 的最大值;
的最大值;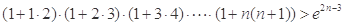 (
(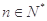 )
) 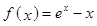 (e为自然对数的底数)
(e为自然对数的底数)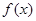 的最小值;
的最小值;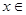
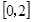 ,不等式
,不等式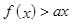 恒成立,求实数
恒成立,求实数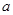 的取值范围.
的取值范围.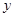 (升)与行驶速度
(升)与行驶速度 。已知甲、乙两地相距100千米。
。已知甲、乙两地相距100千米。
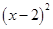 +blnx在(1,+∞)上是减函数,求实数b的取值范围.
+blnx在(1,+∞)上是减函数,求实数b的取值范围.