题目内容
【题目】在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
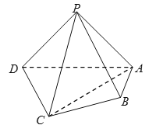
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)见证明;(2)![]() (3)见解析
(3)见解析
【解析】
(1)由面面垂直的性质得![]() 面
面![]() ,即可证明
,即可证明![]() 面
面![]() (2)取
(2)取![]() 中点为
中点为![]() ,连结
,连结![]() ,
,![]() ,证明
,证明![]() , 以
, 以![]() 为原点,如图建系易知
为原点,如图建系易知![]() ,
,![]() ,
,![]() ,
,![]() ,求面
,求面![]() 及面
及面![]() 的法向量,利用二面角的向量公式求解即可(3)假设存在
的法向量,利用二面角的向量公式求解即可(3)假设存在![]() 点使得
点使得![]() ∥面
∥面![]() , 设
, 设![]() ,由
,由![]() ∥面
∥面![]() ,
,![]() 为
为![]() 的法向量,得
的法向量,得![]() ,
,
(1)∵面![]() 面
面![]() ,面
,面![]() 面
面![]() ,
,
∵![]() ,
,![]() 面
面![]() ,∴
,∴![]() 面
面![]() ,
,
∵![]() 面
面![]() , ∴
, ∴![]() ,
,
又![]() ,∴
,∴![]() 面
面![]() ,
,
(2)取![]() 中点为
中点为![]() ,连结
,连结![]() ,
,![]() ,
,
∵![]() , ∴
, ∴![]() ,
,
∵![]() , ∴
, ∴![]() ,
,
以![]() 为原点,如图建系易知
为原点,如图建系易知![]() ,
,![]() ,
,![]() ,
,![]() ,
,
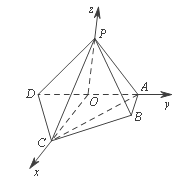
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() 为面
为面![]() 的法向量,令
的法向量,令![]() .
.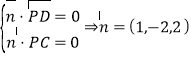 ,
,
设![]() 为面
为面![]() 的法向量,令
的法向量,令![]() .
.
 ,
,
则二面角![]() 余弦值为
余弦值为![]()
故二面角![]() 正弦值为
正弦值为![]()
(3)假设存在![]() 点使得
点使得![]() ∥面
∥面![]() , 设
, 设![]() ,
,![]() ,
,
由(2)知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
有![]() ∴
∴![]()
∵![]() ∥面
∥面![]() ,
,![]() 为
为![]() 的法向量,
的法向量,
∴![]() ,即
,即![]() ,得
,得![]()
综上,存在![]() 点,即当
点,即当![]() 时,
时,![]() 点即为所求.
点即为所求.

练习册系列答案
相关题目