题目内容
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作
作![]() 于点
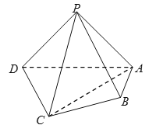
于点![]() ,如图1.已知
,如图1.已知![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() .
.


(1)求抛物线![]() 的方程;
的方程;
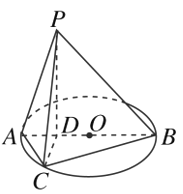
(2)若正方形![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 都在抛物线
都在抛物线![]() 上(如图2),求正方形
上(如图2),求正方形![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)通过借助抛物线的几何性质,设![]() ,通过勾股定理可求得
,通过勾股定理可求得![]() ,借助线段关系可求得
,借助线段关系可求得![]() ,再借助梯形
,再借助梯形![]() 面积公式最终可求得
面积公式最终可求得![]() 值,进而求得抛物线
值,进而求得抛物线![]() 的方程;(2)先通过设而不求得方法分别表示出
的方程;(2)先通过设而不求得方法分别表示出 ,
, ,
, 和直线
和直线![]() 的斜率为
的斜率为![]() 和
和![]() 的斜率
的斜率![]() ,通过正方形的边长关系代换出
,通过正方形的边长关系代换出![]() 与直线
与直线![]() 的斜率
的斜率![]() 的关系,将面积用含
的关系,将面积用含![]() 的式子整体代换表示,最终通过均值不等式处理可求得正方形
的式子整体代换表示,最终通过均值不等式处理可求得正方形![]() 面积的最小值.
面积的最小值.
(1)设![]() ,
,
由已知,则![]() ,
,![]() ,
,
四边形![]() 的面积为
的面积为![]() ,
,
∴![]() ,抛物线
,抛物线![]() 的方程为:
的方程为:![]() .
.
(2)设 ,
, ,
, ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
不妨![]() ,则显然有
,则显然有![]() ,且
,且 .
.
∵![]() ,∴
,∴ .
.
由![]() 得
得![]()
即![]() ,
,
即![]() .
.
将![]() ,
,![]() 代入得
代入得![]() ,
,
∴![]() ,
,
∴![]() .
.
故正方形![]() 面积为
面积为
![]()

 .
.
∵![]() ,∴
,∴ (当且仅当
(当且仅当![]() 时取等).
时取等).
又∵![]() ,
,
∴![]() ,
,
∴![]() (当且仅当
(当且仅当![]() 时取等).从而
时取等).从而![]() ,
,
当且仅当![]() 时取得最小值
时取得最小值![]() .
.

练习册系列答案
相关题目