题目内容
1.设Sn,Tn分别是数列{an}和{bn}的前n项和,已知对于任意n∈N*,都有3an=2Sn+3,数列{bn}是等差数列,且T5=25,b10=19.(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设cn=$\frac{{a}_{n}{b}_{n}}{n(n+1)}$,数列{cn}的前n项和为Rn,求使Rn>2017成立的n的取值范围.
分析 (I)由3an=2Sn+3,可得n=1时,3a1=2a1+3,解得a1=3.n≥2时,3an-1=2Sn-1+3,可得an=3an-1,利用等比数列的通项公式可得an.设等差数列{bn}的公差为d,由T5=25,b10=19.可得5b1+$\frac{5×4}{2}$d=25,b1+9d=19,联立解出即可得出.
(II)由(I)可得:cn=$\frac{{a}_{n}{b}_{n}}{n(n+1)}$=$\frac{(2n-1)•{3}^{n}}{n(n+1)}$=$\frac{[3n-(n+1)]•{3}^{n}}{n(n+1)}$=$\frac{{3}^{n+1}}{n+1}$-$\frac{{3}^{n}}{n}$,利用“裂项求和”方法可得Rn.由于cn>0,故数列{cn}单调递增,即可得出.
解答 解:(I)由3an=2Sn+3,可得n=1时,3a1=2a1+3,解得a1=3.n≥2时,3an-1=2Sn-1+3,可得3an-3an-1=2Sn-2Sn-1=2an,可得an=3an-1,∴数列{an}是等比数列,公比为3,首项为3.∴an=3n.
设等差数列{bn}的公差为d,∵T5=25,b10=19.∴5b1+$\frac{5×4}{2}$d=25,b1+9d=19,
联立解得b1=1,d=2.∴bn=1+2(n-1)=2n-1.
(II)由(I)可得:cn=$\frac{{a}_{n}{b}_{n}}{n(n+1)}$=$\frac{(2n-1)•{3}^{n}}{n(n+1)}$=$\frac{[3n-(n+1)]•{3}^{n}}{n(n+1)}$=$\frac{{3}^{n+1}}{n+1}$-$\frac{{3}^{n}}{n}$,
∴数列{cn}的前n项和为Rn=$(\frac{{3}^{2}}{2}-\frac{3}{1})$+$(\frac{{3}^{3}}{3}-\frac{{3}^{2}}{2})$+…+$(\frac{{3}^{n+1}}{n+1}-\frac{{3}^{n}}{n})$
=$\frac{{3}^{n+1}}{n+1}$-3,
由于cn>0,∴数列{cn}单调递增,
R7=817.125<2017,R8=2184>2017.
∴使Rn>2017成立的n的取值范围是n≥8.
点评 本题考查了数列递推关系、等差数列与等比数列的通项公式、“裂项求和”方法、数列的单调性,考查了推理能力与计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 存在t>0,|f(t)+f(-t)|>f(t)-f(-t) | B. | 存在t>0,|f(t)-f(-t)|>f(t)-f(-t) | ||
| C. | 存在t>0,|f(1+t)+f(1-t)|>f(1+t)+f(1-t) | D. | 存在t>0,|f(1+t)-f(1-t)|>f(1+t)-f(1-t) |
 若将一个质点随机投入如图所示的长方形ABCD中,其中AB=2,BC=1,则质点落在以CD为直径的半圆内的概率是( )
若将一个质点随机投入如图所示的长方形ABCD中,其中AB=2,BC=1,则质点落在以CD为直径的半圆内的概率是( )| A. | $\frac{π}{8}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
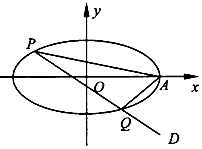 在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的焦距为2,离心率为$\frac{\sqrt{2}}{2}$,椭圆的右顶点为A.
在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的焦距为2,离心率为$\frac{\sqrt{2}}{2}$,椭圆的右顶点为A.