题目内容
a1,a2,…,an∈R+,证明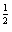 .
.
证明:(a12+a22+…+an2)![]() (1+1+…+1)
(1+1+…+1)![]() ≥a1+a2+…+an?,?
≥a1+a2+…+an?,?
则![]() ≥a1+a2+…+an,?
≥a1+a2+…+an,?
即![]() .
.
再由柯西不等式得(a1+a2+…+an)(![]() +…+
+…+![]() )≥(
)≥(![]() ·
·![]() +
+![]() ·
·![]() +…+
+…+![]() ·
·![]() )2
)2
=n2,?
即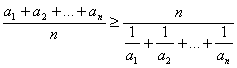 .
.
于是,原不等式得证.
温馨提示
有些问题本身不具备运用柯西不等式的条件,但只要改变一下多项式的结构,认清结构的内部特征,就可以达到利用柯西不等式的目的.

练习册系列答案
相关题目
题目内容
a1,a2,…,an∈R+,证明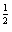 .
.
证明:(a12+a22+…+an2)![]() (1+1+…+1)
(1+1+…+1)![]() ≥a1+a2+…+an?,?
≥a1+a2+…+an?,?
则![]() ≥a1+a2+…+an,?
≥a1+a2+…+an,?
即![]() .
.
再由柯西不等式得(a1+a2+…+an)(![]() +…+
+…+![]() )≥(
)≥(![]() ·
·![]() +
+![]() ·
·![]() +…+
+…+![]() ·
·![]() )2
)2
=n2,?
即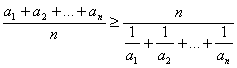 .
.
于是,原不等式得证.
温馨提示
有些问题本身不具备运用柯西不等式的条件,但只要改变一下多项式的结构,认清结构的内部特征,就可以达到利用柯西不等式的目的.
