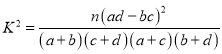题目内容
【题目】已知a R, a0,函数 f (x) eax1 ax ,其中常数e ![]() .
.
(1)求 f (x) 的最小值;
(2)当a ≥1时,求证:对任意 x0 ,都有 xf (x) ≥ 2ln x 1 ax2.
【答案】(1)0;(2)证明见详解.
【解析】
(1)求导,对函数的单调性进行讨论,从而求得最小值;
(2)将不等式恒成问题,进行转换,结合(1)中的结论,构造新的函数,将问题转换为最值的问题即可.
(1)因为![]() ,则
,则![]() ,
,![]()
故![]() 为R上的增函数,令
为R上的增函数,令![]() ,解得
,解得![]()
故当![]() ,
,![]() 单调递减;
单调递减;
当![]() ,
,![]() 单调递增,
单调递增,
则![]()
故函数![]() 的最小值为0.
的最小值为0.
(2)证明:要证明xf (x) ≥ 2ln x 1![]()
等价于证明![]()
由(1)可知:![]() ,即
,即![]()
因为![]() ,故
,故![]()
故等价于证明![]()
即![]()
令![]() ,即证
,即证![]() 恒成立.
恒成立.
又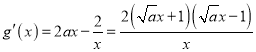
令![]() ,解得
,解得![]()
故当![]() ,
,![]() 单调递减;
单调递减;
当![]() ,
,![]() 单调递增;
单调递增;
故![]()
有因为![]() ,故
,故![]()
故![]() 即证.
即证.
即对任意 x0 ,都有 xf (x) ≥ 2ln x 1 ax2.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案【题目】某校实行选科走班制度,张毅同学的选择是物理生物政治这三科,且物理在 A 层班级,生物在 B 层班级,该校周一上午课程安排如下表所示,张毅选择三个科目的课各上一节, 另外一节上自习,则他不同的选课方法有( )
第一节 | 第二节 | 第三节 | 第四节 |
地理 B 层 2 班 | 化学 A 层 3 班 | 地理 A 层 1 班 | 化学 A 层 4 班 |
生物 A 层 1 班 | 化学 B 层 2 班 | 生物 B 层 2 班 | 历史 B 层 1 班 |
物理 A 层 1 班 | 生物 A 层 3 班 | 物理 A 层 2 班 | 生物 A 层 4 班 |
物理 B 层 2 班 | 生物 B 层 1 班 | 物理 B 层 1 班 | 物理 A 层 4 班 |
政治 1 班 | 物理 A 层 3 班 | 政治 2 班 | 政治 3 班 |
A.8 种B.10 种C.12 种D.14 种
【题目】某学校为了解学生假期参与志愿服务活动的情况,随机调查了![]() 名男生,
名男生,![]() 名女生,得到他们一周参与志愿服务活动时间的统计数据如右表(单位:人):
名女生,得到他们一周参与志愿服务活动时间的统计数据如右表(单位:人):
超过 | 不超过 | |
男 |
|
|
女 |
|
|
(1)能否有![]() 的把握认为该校学生一周参与志愿服务活动时间是否超过
的把握认为该校学生一周参与志愿服务活动时间是否超过![]() 小时与性别有关?
小时与性别有关?
(2)以这![]() 名学生参与志愿服务活动时间超过
名学生参与志愿服务活动时间超过![]() 小时的频率作为该事件发生的概率,现从该校学生中随机抽查
小时的频率作为该事件发生的概率,现从该校学生中随机抽查![]() 名学生,试估计这
名学生,试估计这![]() 名学生中一周参与志愿服务活动时间超过
名学生中一周参与志愿服务活动时间超过![]() 小时的人数.
小时的人数.
附:
|
|
|
|
|
|
|
|