题目内容
【题目】如图,四棱锥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为等边三角形,平面
为等边三角形,平面![]() 平面
平面![]() ,
,![]() 为
为![]() 中点.
中点.
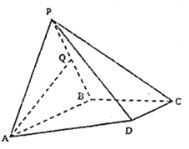
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)证明![]() 及
及![]() ,即可证明:
,即可证明:![]() 平面
平面![]() ,问题得证。
,问题得证。
(2)建立空间直角坐标系,由(1)得![]() 为平面
为平面![]() 的法向量,求得平面
的法向量,求得平面![]() 的法向量为
的法向量为![]() ,利用空间向量夹角的数量积表示即可求得二面角
,利用空间向量夹角的数量积表示即可求得二面角![]() 的余弦值.
的余弦值.
(1)证明:因为![]() ,
,![]() ,
,
所以![]() ,
,
又平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() 为
为![]() 中点,且
中点,且![]() 为等边三角形,所以
为等边三角形,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)取![]() 中点为
中点为![]() ,连接
,连接![]() ,因为
,因为![]() 为等边三角形,所以
为等边三角形,所以![]() ,
,
因为平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() ,由
,由![]() ,
,![]() ,
,
可知![]() ,所以
,所以![]() .
.
以![]() 中点
中点![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() .
.
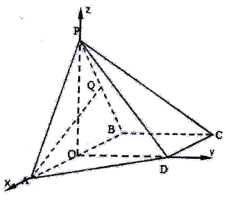
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
由(1)知,![]() 为平面
为平面![]() 的法向量,
的法向量,
因为![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,
所以![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由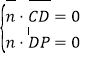 ,得
,得![]() ,
,
取![]() ,则
,则![]() .
.
所以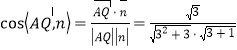
![]() .
.
因为二面角![]() 为钝角,
为钝角,
所以,二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有6人 | 6 | 6 | 3 | 1 | 2 | 0 |
选考方案待确定的有8人 | 5 | 4 | 0 | 1 | 2 | 1 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 0 | 0 | 1 | 1 |
(Ⅰ)试估计该学校高一年级确定选考生物的学生有多少人?
(Ⅱ)写出选考方案确定的男生中选择“物理、化学和地理”的人数.(直接写出结果)
(Ⅲ)从选考方案确定的男生中任选2名,试求出这2名学生选考科目完全相同的概率.


