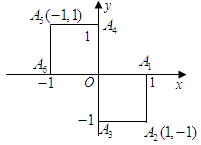题目内容
我校社团联即将举行一届象棋比赛,规则如下:两名选手比赛时,每局胜者得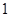 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多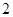 分或打满
分或打满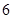 局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为
局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为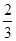 ,且各局比赛胜负互不影响.
,且各局比赛胜负互不影响.
(Ⅰ)求比赛进行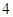 局结束,且乙比甲多得
局结束,且乙比甲多得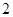 分的概率;
分的概率;
(Ⅱ)设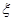 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量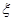 的分布列和数学期望.
的分布列和数学期望.
(Ⅰ) ;(Ⅱ)随机变量
;(Ⅱ)随机变量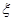 的分布列为
的分布列为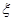
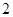
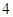
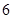





解析试题分析:(Ⅰ)这是一个独立重复试验,比赛进行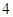 局结束,且乙比甲多得
局结束,且乙比甲多得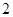 分,只能是前两局乙胜一局,3,4局乙连胜,根据独立重复试验从而求出,值得注意的是,做这一类题,一定分析清楚,否则容易出错;(Ⅱ)设
分,只能是前两局乙胜一局,3,4局乙连胜,根据独立重复试验从而求出,值得注意的是,做这一类题,一定分析清楚,否则容易出错;(Ⅱ)设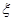 表示比赛停止时已比赛的局数,
表示比赛停止时已比赛的局数,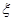 只能取值
只能取值 ,不能为3,5,分别求出
,不能为3,5,分别求出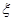 的取值为
的取值为 的概率,列分布列,从而求出数学期望,易错点为
的概率,列分布列,从而求出数学期望,易错点为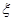 的取值不正确,导致分布列错误。
的取值不正确,导致分布列错误。
试题解析:(Ⅰ)由题意知,乙每局获胜的概率皆为 .比赛进行
.比赛进行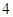 局结束,且乙比甲多得
局结束,且乙比甲多得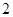 分即头两局乙胜一局,3,4局连胜,则
分即头两局乙胜一局,3,4局连胜,则 .
.
(Ⅱ)由题意知,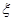 的取值为
的取值为 .则
.则
 ,
,  ,所以随机变量
,所以随机变量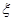 的分布列为
的分布列为
则





考点:本题考查独立重复事件的概率计算、离散型随机变量的分布列、期望,考查学生的逻辑推理能力以及基本运算能力.

练习册系列答案
相关题目
德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
| 课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 |
| 合格的概率 |  |  |  |  |
(2)记
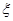 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求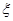 的分布列及期望
的分布列及期望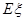 .
.  ,
,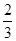 ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.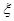 ,求
,求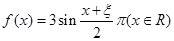 是偶函数”为事件D,求事件D发生的概率.
是偶函数”为事件D,求事件D发生的概率.
 的值;
的值;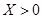 就去打球;若
就去打球;若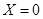 就去唱歌;若
就去唱歌;若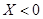 就去下棋.
就去下棋.