题目内容
17．已知集合$A=\{x|\frac{x+1}{x-3}＜0\}$，B={x|x-x2＞0}，则（ ）| A． | A?B | B． | A=B | C． | A∩B=B | D． | A∪B=（0，3） |
分析 求出A与B中不等式的解集确定出A与B，找出A与B的交集即可．
解答 解：由A中不等式变形得：（x+1）（x-3）＜0，
解得：-1＜x＜3，即A=（-1，3），
由B中不等式变形得：x（x-1）＜0，
解得：0＜x＜1，即B=（0，1），
∴A∩B=（0，1）=B，
故选：C．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
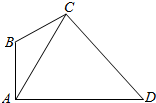在如图所示的四边形ABCD中，已知AB⊥AD，∠ABC=120°，∠ACD=60°，AD=2$\sqrt{3}$，设∠ACB=θ，点C到AD的距离为h．
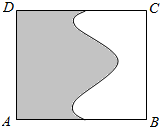如图面积为4的矩形ABCD中有一个阴影部分，若往矩形ABCD投掷1000个点，落在矩形ABCD的非阴影部分中的点数为400个，试估计阴影部分的面积为2.4．