题目内容
6．
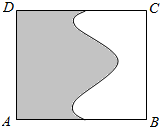如图面积为4的矩形ABCD中有一个阴影部分，若往矩形ABCD投掷1000个点，落在矩形ABCD的非阴影部分中的点数为400个，试估计阴影部分的面积为2.4．
分析 根据若往矩形ABCD投掷1000个点，落在矩形ABCD的非阴影部分中的点数为600个可估计落在阴影部分的概率，而落在阴影部分的概率等于阴影部分的面积与矩形的面积比，从而可求出所求．
解答 解：根据几何概率的计算公式可得，向距形内随机投掷1000个点，落在矩形ABCD的非阴影部分中的点数为400个，则落在矩形ABCD的阴影部分中的点数为600个，
设阴影部分的面积为S，落在阴影部分为事件A，
∴落在阴影部分的概率P（A）=$\frac{600}{1000}$=$\frac{S}{4}$，解得S=2.4．
故答案为：2.4
点评 本题考查了几何概型，解答此题的关键在于明确测度比是面积比．对于几何概型常见的测度是长度之比，面积之比，体积之比，角度之比，要根据题意合理的判断和选择是哪一种测度进行求解．属于中档题．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
17．已知集合$A=\{x|\frac{x+1}{x-3}＜0\}$，B={x|x-x2＞0}，则（ ）
| A． | A?B | B． | A=B | C． | A∩B=B | D． | A∪B=（0，3） |
11．下列说法中正确的是（ ）
| A． | “若$\overrightarrow a•\overrightarrow b=0$，则$\overrightarrow a⊥\overrightarrow b$”的否命题是“若$\overrightarrow a•\overrightarrow b≠0$，则$\overrightarrow a⊥\overrightarrow b$” | |
| B． | 命题“?x∈R，恒有x2+1＞0”的否定是“?x0∈R，使得${x_0}^2+1＜0$” | |
| C． | ?m∈R，使函数f（x）=x2+mx（x∈R）是奇函数 | |
| D． | 设p，q是简单命题，若p∧q是真命题，则（￢p）∨q也是真命题 |