题目内容

已知方程f(x)=x3+ax2+bx+c=0的三个实根可分别作为一个椭圆、一双曲线、一抛物线的离心率.

(1)求a+b+c的值;

(2)求的取值范围.

解:(1)由抛物线的离心率为1,知方程f(x)=0有一个根为1,

即有f(1)=1+a+b+c=0,所以a+b+c=-1.

(2)由(1)c=-1-a-b,f(x)=x3+ax2+bx+c=-1-a-b=(x-1)［x2+(1+a)x+a+b+1］.

依题意可知方程g(x)=x2+(1+a)x+a+b+1=0有一个大于0小于1的根与一个大于1的根.

借助二次函数的图象特征,知即

在平面直角坐标系aOb内,(a,b)所表示的平面区域为图中的阴影部分,其中A点坐标为(-2,1),k OA=.

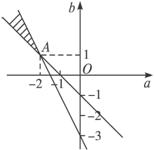
求的范围可转化为求区域内的点与原点的连线所在直线的斜率的取值范围.

由图形可知:-2＜＜,

所以的取值范围是(-2,).

(其他解法请相应给分).

练习册系列答案
相关题目
已知函数f(x)=ln(2+3x)-
3
2
x2．
（I）求f（x）在[0，1]上的最大值；
（II）若对任意的实数x∈[
1
6
，
1
2
]，不等式|a-lnx|+ln[f'（x）+3x]＞0恒成立，求实数a的取值范围；
（III）若关于x的方程f（x）=-2x+b在[0，1]上恰有两个不同的实根，求实数b的取值范围．
已知函数f(x)=ax+
bx-1
-a(a∈R，a≠0)在x=3处的切线方程为（2a-1）x-2y+3=0
（1）若g（x）=f（x+1），求证：曲线g（x）上的任意一点处的切线与直线x=0和直线y=ax围成的三角形面积为定值；
（2）若f（3）=3，是否存在实数m，k，使得f（x）+f（m-x）=k对于定义域内的任意x都成立；
已知函数f（x）=ex（e为自然对数的底数），g（x）=ln（f（x）+a）（a为常数），g（x）是实数集R上的奇函数．
（1）求证：f（x）≥x+1（x∈R）；
（2）讨论关于x的方程：lng（x）=g（x）•（x2-2ex+m）（m∈R）的根的个数；
（3）设n∈N*，证明：(
1
n
)n+(
2
n
)n+(
3
n
)n+…+(
n
n
)n＜
e
e-1
（e为自然对数的底数）．
已知函数f(x)=x+
ax
-a，
（1）若方程f（x）=0有正根，求实数a的取值范围；
（2）设g（x）=|xf（x）|，且g（x）在区间[0，1]上是减函数，求实数a的取值范围．
已知函数f(x)=ax+
2
x
+6，其中a为实常数．
（1）若f（x）＞3x在（1，+∞）上恒成立，求a的取值范围；
（2）已知a=
3
4
，P1，P2是函数f（x）图象上两点，若在点P1，P2处的两条切线相互平行，求这两条切线间距离的最大值；
（3）设定义在区间D上的函数y=s（x）在点P（x0，y0）处的切线方程为l：y=t（x），当x≠x0时，若
s(x)-t(x)
x-x0
＞0在D上恒成立，则称点P为函数y=s（x）的“好点”．试问函数g（x）=x2f（x）是否存在“好点”．若存在，请求出所有“好点”坐标，若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网