题目内容
13.已知数列{an}满足a1=1,nan=(n-1)an-1(n≥2),求数列{an}的通项公式.分析 由已知得a1=1,$\frac{{a}_{n}}{{a}_{n-1}}=\frac{n-1}{n}$,n≥2,由此利用累乘法能求出数列{an}的通项公式.
解答 解:∵数列{an}满足a1=1,nan=(n-1)an-1(n≥2),
∴$\frac{{a}_{n}}{{a}_{n-1}}=\frac{n-1}{n}$,n≥2,
∴${a}_{n}={a}_{1}×\frac{{a}_{2}}{{a}_{1}}×\frac{{a}_{3}}{{a}_{2}}×…×\frac{{a}_{n}}{{a}_{n-1}}$
=1×$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}$×…×$\frac{n-1}{n}$=$\frac{1}{n}$.
故数列{an}的通项公式为an=$\frac{1}{n}$.
点评 本题考查数列的通项公式的求法,是基础题,解题时要注意累乘法的合理运用.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
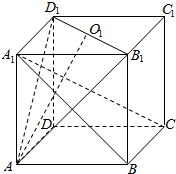 已知点O1是正方体ABCD-A1B1C1D1的上底面的中心,求证:对角线A1C与平面AD1B1的交点P一定在AO1上.
已知点O1是正方体ABCD-A1B1C1D1的上底面的中心,求证:对角线A1C与平面AD1B1的交点P一定在AO1上.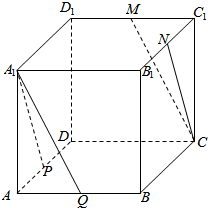 在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证:
在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证: