题目内容
已知函数
 ,且
,且 能表示成一个奇函数
能表示成一个奇函数 和一个偶函数
和一个偶函数 的和.
的和.
(1)求 和
和 的解析式.
的解析式.
(2)命题 :函数
:函数 在区间
在区间 上是增函数;命题
上是增函数;命题 :函数
:函数 是减函数,如果命题
是减函数,如果命题 、
、 有且仅有一个是真命题,求实数
有且仅有一个是真命题,求实数 的取值范围.
的取值范围.
(3)在(2)的条件下,比较 和
和 的大小.
的大小.
(1) ;(2)
;(2) ;(3)
;(3)
解析试题分析:(1) ,
, ,
,


解得
(2) 在
在 上是增函数
上是增函数 ,解得
,解得 或
或 且
且
又 是减函数
是减函数 且
且
又命题 有且仅有一个是真命题
有且仅有一个是真命题
(3)
由(2)知

设函数
 ,
, 在区间
在区间 上为增函数
上为增函数
又
 时,
时, 即:
即:
考点:本题考查了函数的解析式及单调性的运用
点评:对函数的考查主要有:①考查函数的表示法、定义域、值域、单调性、奇偶性、反函数和函数的图象。②函数与方程、不等式、数列是相互关联的概念,通过对实际问题的抽象分析,建立相应的函数模型并用来解决问题,是考试的热点。③考查运用函数的思想来观察问题、分析问题和解决问题,渗透数形结合和分类讨论的基本数学思想。

练习册系列答案
相关题目
 .
.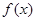 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围;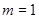 ,
,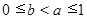 时,证明:
时,证明: .
.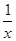 在(0,1)上是减函数.
在(0,1)上是减函数.

 时的值域;
时的值域; 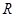 的函数
的函数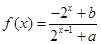 是奇函数。
是奇函数。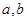 的值;
的值;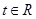 ,不等式
,不等式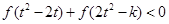 恒成立,求
恒成立,求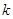 的取值范围;
的取值范围; 在
在 上是偶函数,其图象关于直线
上是偶函数,其图象关于直线 对称,且在区间
对称,且在区间 上是单调函数,求
上是单调函数,求 和
和 的值.
的值. 。
。
 )上存在极值,其中a>0,求实数a的取值范围;
)上存在极值,其中a>0,求实数a的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 。
。 在定义域内为增函数,求实数
在定义域内为增函数,求实数 的取值范围;
的取值范围; ,若函数
,若函数 存在两个零点
存在两个零点 ,且满足
,且满足 ,问:函数
,问:函数 处的切线能否平行于
处的切线能否平行于 轴?若能,求出该切线方程;若不能,请说明理由。
轴?若能,求出该切线方程;若不能,请说明理由。