题目内容
已知定点A(4，0)和圆x2+y2=4上的动点B，点P分AB之比为 2∶1，求点P的轨迹方程.
所求轨迹方程为(x－
)2+y2=
.
)2+y2=.设点P(x,y)、B(x0,y0)，由
=2，找出x、y与x0、y0的关系.
利用已知曲线方程消去x0、y0得到x、y的关系.
设动点P(x,y)及圆上点B(x0,y0).
∵λ==2,
∴
代入圆的方程x2+y2=4
得(
)2+
=4,
即(x－)2+y2=.
∴所求轨迹方程为(x－)2+y2=.
=2，找出x、y与x0、y0的关系.利用已知曲线方程消去x0、y0得到x、y的关系.
设动点P(x,y)及圆上点B(x0,y0).
∵λ=
=2,∴
代入圆的方程x2+y2=4
得(
)2+=4,即(x－
)2+y2=.∴所求轨迹方程为(x－
)2+y2=.
练习册系列答案
备战中考寒假系列答案
相关题目
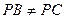．设A，D分别是边PB，PC上的点，连接AC，BD，相交于点O. 过点O分别作OE⊥AB，OF⊥CD，垂足分别为E，F，线段BC，AD的中点分别为M，N．
；
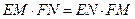的三个顶点的坐标分别是
，
，
,2)
，
．
．
与圆
交于
两点，则
（
是
