题目内容
给定锐角三角形PBC,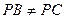 .设A,D分别是边PB,PC上的点,连接AC,BD,相交于点O. 过点O分别作OE⊥AB,OF⊥CD,垂足分别为E,F,线段BC,AD的中点分别为M,N.
.设A,D分别是边PB,PC上的点,连接AC,BD,相交于点O. 过点O分别作OE⊥AB,OF⊥CD,垂足分别为E,F,线段BC,AD的中点分别为M,N.
(1)若A,B,C,D四点共圆,求证: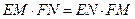 ;
;
(2)若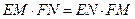 ,是否一定有A,B,C,D四点共圆?证明你的结论.
,是否一定有A,B,C,D四点共圆?证明你的结论.
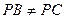 .设A,D分别是边PB,PC上的点,连接AC,BD,相交于点O. 过点O分别作OE⊥AB,OF⊥CD,垂足分别为E,F,线段BC,AD的中点分别为M,N.
.设A,D分别是边PB,PC上的点,连接AC,BD,相交于点O. 过点O分别作OE⊥AB,OF⊥CD,垂足分别为E,F,线段BC,AD的中点分别为M,N.(1)若A,B,C,D四点共圆,求证:
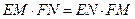 ;
;(2)若
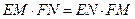 ,是否一定有A,B,C,D四点共圆?证明你的结论.
,是否一定有A,B,C,D四点共圆?证明你的结论.见解析
 (1)设Q,R分别是OB,OC的中点,连接EQ,MQ,FR,MR,则
(1)设Q,R分别是OB,OC的中点,连接EQ,MQ,FR,MR,则
 ,
,又OQMR是平行四边形,
所以
 ,
,由题设A,B,C,D四点共圆,
所以
 ,
, 

于是
 ,
,所以
 ,
,故
 ,
,所以 EM=FM,


同理可得 EN=FN,
所以
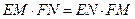 .
.(2)答案是否定的.
当AD∥BC时,由于
 ,所以A,B,C,D四点不共圆,但此时仍然有
,所以A,B,C,D四点不共圆,但此时仍然有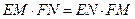 ,证明如下:
,证明如下:如图2所示,设S,Q分别是OA,OB的中点,连接ES,EQ,MQ,NS,则
 ,
,所以
 .
. 
 ①
①又
 ,
,所以
 . ②
. ②而AD∥BC,所以
 , ③
, ③由①,②,③得
 .
.因为
 ,
,
 ,
,即
 ,
,所以
 ~
~ ,
, 

故
 (由②).
(由②).同理可得,
 ,
,所以
 ,
,从而
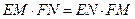 .
.
练习册系列答案
相关题目
 外切,且与直线
外切,且与直线 相切于点
相切于点 的圆的方程.
的圆的方程.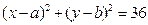 的曲线经过点
的曲线经过点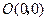 和点
和点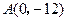 ,求
,求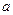 ,
,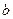 的值.
的值.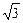 y=0,求x+y的最小值.
y=0,求x+y的最小值.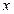 轴相切,半径为
轴相切,半径为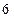 ,圆心的横坐标为
,圆心的横坐标为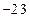 的圆的方程为( ).
的圆的方程为( ).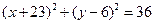
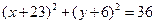
 满足
满足 ,若不等式
,若不等式 对任意的
对任意的 的取值范围是( )
的取值范围是( )

 ,+∞)
,+∞)
 , +∞)
, +∞) 的圆心的轨迹方程是 .
的圆心的轨迹方程是 .