Question

【题目】如图，网格纸上小正方形的边长为1，粗线画出的是某四面体的三视图，则该四面体的外接球半径为（ ）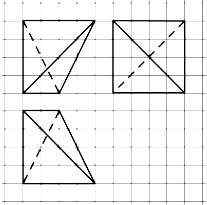

A.2
B.
C.
D.2

Answer 1

【答案】C
【解析】
解：由三视图知几何体是三棱锥A﹣BCD，为棱长为4的正方体一部分，
直观图如图所示：

由正方体的性质可得，AB=AD=BD=4 ，
AC=BC= =2 ，CD= =6，
设三棱锥C﹣ABD的外接球球心是O，设半径是R，
取AB的中点E，连接CE、DE，如图所示：

设OA=OB=OC=OD=R，△ABD是等边三角形，
∴O在底面△ABD的射影是△ABD中心F，
∵DE⊥BE，BE=2 ，∴DE= = ，
同理可得，CE=2 ，则满足CE2+DE2=CD2 ， 即CE⊥DE，
在RT△CED中，设OF=x，
∵F是等边△ABD的中心，
∴ ，
，
则 ，
∴ ，解得x= ，
代入其中一个方程得，R= = = ，
∴该四面体的外接球半径是 ，
故选：C．
根据三视图知几何体是三棱锥为棱长为4的正方体一部分，画出直观图，由正方体的性质求出棱长、判断出各面形状，画出三棱锥C﹣ABD以及外接球，由△ABD是等边三角形，判断出球心O在△ABD的射影的位置，判断线与线的位置关系，设出未知数画出平面图形，利用勾股定理列出方程组，求出该四面体的外接球半径．