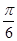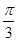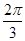题目内容
在△ABC中,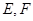 分别是
分别是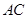 ,
,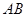 的中点,且
的中点,且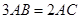 ,若
,若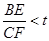 恒成立,则
恒成立,则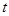 的最小值为( )
的最小值为( )
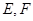 分别是
分别是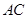 ,
,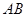 的中点,且
的中点,且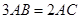 ,若
,若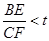 恒成立,则
恒成立,则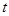 的最小值为( )
的最小值为( )A. | B. | C.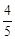 | D. |
A
试题分析:如图所示:
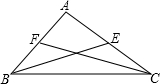
∵3AB=2AC,∴AC=
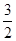 AB,
AB,又E、F分别为AC、AB的中点,
∴AE=
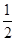 AC,AF=
AC,AF=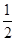 AB,
AB,∴在△ABE中,由余弦定理得:BE2=AB2+AE2-2AB•AE•cosA
=AB2+(
 AB)2-2AB•
AB)2-2AB• AB•cosA=
AB•cosA=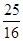 AB2-
AB2-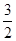 AB2cosA,
AB2cosA,在△ACF中,由余弦定理得:CF2=AF2+AC2-2AF•AC•cosA
=(
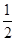 AB)2+(
AB)2+(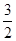 AB)2-2•
AB)2-2•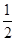 AB•
AB•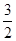 AB•cosA=
AB•cosA=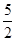 AB2-
AB2-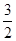 AB2cosA,
AB2cosA,∴
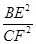 =
=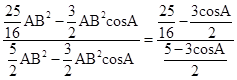 ,
,∴
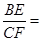
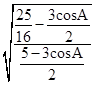 =
= .
.∵当cosA取最小值时,
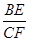 最大,
最大,∴当A→π时,cosA→-1,此时
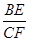 达到最大值,最大值为
达到最大值,最大值为 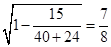 ,
,故
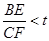 恒成立,t的最小值为
恒成立,t的最小值为 .选A.
.选A.点评:中档题,不等式恒成立问题,往往通过“分离参数”,转化成求函数的最值问题,解答本题的关键是,熟练掌握余弦定理,利用余弦定理建立三角形的边角关系。

练习册系列答案
相关题目
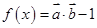 ,其中向量
,其中向量 ,
,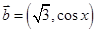 ,
, .在
.在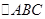 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为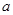 ,
,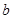 ,
,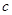 .
.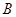 的取值范围及此时函数
的取值范围及此时函数 的值域;
的值域;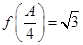 ,
, 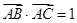 ,求
,求 的三个内角A、B、C成等差数列,
的三个内角A、B、C成等差数列, ,则
,则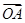 =(1,7),
=(1,7), =(5,1),
=(5,1),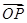 =(2,1),点Q为直线OP上一动点.
=(2,1),点Q为直线OP上一动点.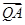 ·
· 取得最小值时,求
取得最小值时,求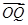 坐标;
坐标;

 ,且
,且 则向量
则向量 与
与 的夹角为( )
的夹角为( )



 中,已知
中,已知 ,
, 为
为 的中点,若
的中点,若 为正方形内(含边界)任意一点,则
为正方形内(含边界)任意一点,则 的取值范围是
的取值范围是 
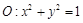 和三点,
和三点,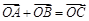 ,
,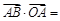
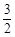 B.
B.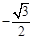 C.
C.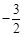 D.
D.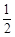
 ,则
,则 =( )
=( )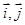 满足
满足 ,则
,则