题目内容
14.等比数列{an}中,a1+a2=3,a4+a5=24,则a7=128.分析 根据题意,设等比数列{an}的首项为a1,公比为q,则有$\left\{\begin{array}{l}{{a}_{1}+{a}_{1}q=3}\\{{a}_{1}{q}^{3}+{a}_{1}{q}^{4}=24}\end{array}\right.$,解可得a1与q,由等比数列的通项公式计算可得答案.
解答 解:根据题意,设等比数列{an}的首项为a1,公比为q,
则有$\left\{\begin{array}{l}{{a}_{1}+{a}_{1}q=3}\\{{a}_{1}{q}^{3}+{a}_{1}{q}^{4}=24}\end{array}\right.$,解可得$\left\{\begin{array}{l}{{a}_{1}=1}\\{q=2}\end{array}\right.$,
则a7=a1q6=1×26=128,
故答案为:128.
点评 本题考查等比数列的通项公式,一般设出等比数列的首项与公比,进而解方程得到该数列的通项公式.

练习册系列答案
相关题目
4.已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,-2),则与向量$\overrightarrow{b}$-$\overrightarrow{a}$垂直的单位向量为( )
| A. | (-2,1)或(2,-1) | B. | (-1,2)或(1,-2) | ||
| C. | (-$\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$)或($\frac{\sqrt{5}}{5}$,-$\frac{2\sqrt{5}}{5}$) | D. | (-$\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$)或($\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$) |
5.在△ABC中,内角A,B,C的对边分别为a,b,c,且acosB=bcosA,a2+b2=c2+ab,则△ABC是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
2.集合M={x|1<x+1≤3},N={x|x2-2x-3>0},则(∁RM)∩(∁RN)等于( )
| A. | (-1,3) | B. | (-1,0)∪(2,3) | C. | (-1,0]∪[2,3) | D. | [-1,0]∪(2,3] |
6.已知f(x)=1+x-sinx,则f(2),f(3),f(π)的大小关系正确的是( )
| A. | f(2)>f(3)>f(π) | B. | f(3)>f(2)>f(π) | C. | f(2)>f(π)>f(3) | D. | f(π)>f(3)>f(2) |
4.两定点F1(-3,0),F2(3,0),P为曲线$\frac{|x|}{5}+\frac{|y|}{4}$=1上任意一点,则( )
| A. | |PF1|+|PF2|≥10 | B. | |PF1|+|PF2|≤10 | C. | |PF1|+|PF2|>10 | D. | |PF1|+|PF2|<10 |
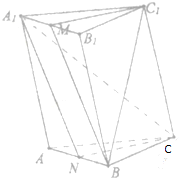 在三棱柱ABC-A1B1C1中,上下两个底面平行,侧面是平行四边形,N是AB的中点,M是A1B1的中点,求证:平面A1NC∥平面BMC1.
在三棱柱ABC-A1B1C1中,上下两个底面平行,侧面是平行四边形,N是AB的中点,M是A1B1的中点,求证:平面A1NC∥平面BMC1.