题目内容
设m.n∈R,给出下列命题:
(1)m<n<0?m2<n2(2)ma2<na2?m<n(3) ,(4)
,(4)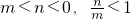 .
.
其中正确的命题有
- A.(1)(4)
- B.(2)(4)
- C.(2)(3)
- D.(3)(4)
B
分析:通过举反例进行判断(1)不对,利用不等式两边同乘以一个数的性质判断(2)、(3),利用做差法进行判断.
解答:(1)当m=-2,n=-1时,m2=4,n2=1,故(1)不对;
(2)因为a2>0,所以两边同除以a2,不等号方向不变,故(2)正确;
(3)当n<0时,有ma>na,故(3)不对;
(4)∵ ,且m<n<0,∴n-m>0
,且m<n<0,∴n-m>0
∴ ,即
,即 ,则
,则 ,故(4)正确.
,故(4)正确.
故选B.
点评:本题考查了不等式性质的应用,对于选择题可以用特值法进行判断,或者利用做差法进行判断.
分析:通过举反例进行判断(1)不对,利用不等式两边同乘以一个数的性质判断(2)、(3),利用做差法进行判断.
解答:(1)当m=-2,n=-1时,m2=4,n2=1,故(1)不对;
(2)因为a2>0,所以两边同除以a2,不等号方向不变,故(2)正确;
(3)当n<0时,有ma>na,故(3)不对;
(4)∵
 ,且m<n<0,∴n-m>0
,且m<n<0,∴n-m>0∴
 ,即
,即 ,则
,则 ,故(4)正确.
,故(4)正确.故选B.
点评:本题考查了不等式性质的应用,对于选择题可以用特值法进行判断,或者利用做差法进行判断.

练习册系列答案
相关题目
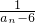 -
-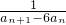 ,数列{bn}的前n项和为Tn,求证:-
,数列{bn}的前n项和为Tn,求证:- ≤Tn<-
≤Tn<- .
.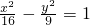 的右支上一点,M,N分别是圆(x+5)2+y2=1和圆(x-5)2+y2=4上的点,则|PM|-|PN|的最大值为
的右支上一点,M,N分别是圆(x+5)2+y2=1和圆(x-5)2+y2=4上的点,则|PM|-|PN|的最大值为 的一条渐近线与抛物线C2:y2=2px(p>0)的一个交点在x轴上的射影在抛物线C2的焦点的右侧,则双曲线C1的离心率的取值范围是________.
的一条渐近线与抛物线C2:y2=2px(p>0)的一个交点在x轴上的射影在抛物线C2的焦点的右侧,则双曲线C1的离心率的取值范围是________. 等于
等于



 已知正三棱柱(侧棱与底面垂直,底面是正三角形)的高与底面边长均为2,其直观图和正(主)视图如下,则它的左(侧)视图的面积是________.
已知正三棱柱(侧棱与底面垂直,底面是正三角形)的高与底面边长均为2,其直观图和正(主)视图如下,则它的左(侧)视图的面积是________.