题目内容
数列{an}满足a1=2,an+1=an2+6an+6(n∈N*).
(I)求数列{an}的通项公式;
(II)设bn=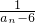 -
-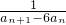 ,数列{bn}的前n项和为Tn,求证:-
,数列{bn}的前n项和为Tn,求证:- ≤Tn<-
≤Tn<- .
.
(I)解:由an+1=an2+6an+6得:an+1+3=(an+3)2
两边同时取对数得:lg(an+1+3)=2lg(an+3)
∴数列{lg(an+3)}是以lg(a1+3)=lg5为首项以2为公比的等比数列
∴lg(an+3)=lg5•2n-1
∴an= -3 …(4分)
-3 …(4分)
(II)证明:∵an2+6an=an+1-6,
∴bn=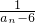 -
- …(6分)
…(6分)
∴Tn= -
-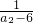 +…+
+…+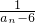 -
- =
= -
- =-
=- -
-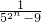 …(9分)
…(9分)
∵n≥1,∴2n≥2,∴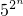 ≥25
≥25
∴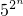 -9≥16,∴0<
-9≥16,∴0<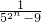 ≤
≤
∴- ≤-
≤-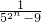 <0,
<0,
∴- ≤-
≤- -
-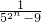 <-
<-
∴- ≤Tn<-
≤Tn<- …(12分)
…(12分)
分析:(I)确定数列{lg(an+3)}是以lg(a1+3)=lg5为首项,以2为公比的等比数列,从而可得数列{an}的通项公式;
(II)确定数列的通项,再求和,从而可得结论.
点评:本题考查数列与不等式的综合,考查等比数列的通项,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.
两边同时取对数得:lg(an+1+3)=2lg(an+3)
∴数列{lg(an+3)}是以lg(a1+3)=lg5为首项以2为公比的等比数列
∴lg(an+3)=lg5•2n-1
∴an=
 -3 …(4分)
-3 …(4分)(II)证明:∵an2+6an=an+1-6,
∴bn=
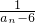 -
- …(6分)
…(6分)∴Tn=
 -
-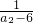 +…+
+…+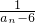 -
- =
= -
- =-
=- -
-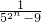 …(9分)
…(9分)∵n≥1,∴2n≥2,∴
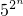 ≥25
≥25∴
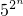 -9≥16,∴0<
-9≥16,∴0<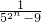 ≤
≤
∴-
 ≤-
≤-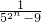 <0,
<0,∴-
 ≤-
≤- -
-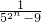 <-
<-
∴-
 ≤Tn<-
≤Tn<- …(12分)
…(12分)分析:(I)确定数列{lg(an+3)}是以lg(a1+3)=lg5为首项,以2为公比的等比数列,从而可得数列{an}的通项公式;
(II)确定数列的通项,再求和,从而可得结论.
点评:本题考查数列与不等式的综合,考查等比数列的通项,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目