题目内容
(本小题满分12分)如图,已知直线l: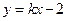 与抛物线C:
与抛物线C: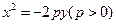 交于A,B两点,
交于A,B两点,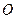 为坐标原点,
为坐标原点,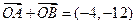 。
。
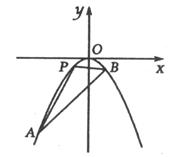
(Ⅰ)求直线l和抛物线C的方程;
(Ⅱ)抛物线上一动点P从A到B运动时,
求△ABP面积最大值.
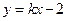 与抛物线C:
与抛物线C: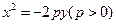 交于A,B两点,
交于A,B两点,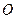 为坐标原点,
为坐标原点,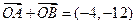 。
。
(Ⅰ)求直线l和抛物线C的方程;
(Ⅱ)抛物线上一动点P从A到B运动时,
求△ABP面积最大值.
(1) ;(2)
;(2)
 ;(2)
;(2)
解:(Ⅰ)由 得,
得, …………2分
…………2分
设 则
则
因为 =
=
所以 解得
解得 ………………4分
………………4分
所以直线 的方程为
的方程为 抛物线C的方程为
抛物线C的方程为 …………6分
…………6分
(Ⅱ)方法1:设 依题意,抛物线过P的切线与
依题意,抛物线过P的切线与 平行时,△APB面积最大,
平行时,△APB面积最大,
 ,所以
,所以
 所以
所以
此时 到直线
到直线 的距离
的距离 ………………8分
………………8分
由 得,
得, ………………………9分
………………………9分

∴△ABP的面积最大值为 。 ………………………12分
。 ………………………12分
(Ⅱ)方法2:由 得,
得, ……………………8分
……………………8分
 ……9分
……9分
设 ,
,
因为 为定值,当
为定值,当 到直线
到直线 的距离
的距离 最大时,△ABP的面积最大,
最大时,△ABP的面积最大,
 ………………………10分
………………………10分
因为 ,所以当
,所以当 时,
时, max=
max= ,此时
,此时
∴△ABP的面积最大值为 .……………………………12分
.……………………………12分
 得,
得, …………2分
…………2分设
 则
则
因为
 =
=
所以
 解得
解得 ………………4分
………………4分所以直线
 的方程为
的方程为 抛物线C的方程为
抛物线C的方程为 …………6分
…………6分(Ⅱ)方法1:设
 依题意,抛物线过P的切线与
依题意,抛物线过P的切线与 平行时,△APB面积最大,
平行时,△APB面积最大, ,所以
,所以
 所以
所以
此时
 到直线
到直线 的距离
的距离 ………………8分
………………8分由
 得,
得, ………………………9分
………………………9分
∴△ABP的面积最大值为
 。 ………………………12分
。 ………………………12分(Ⅱ)方法2:由
 得,
得, ……………………8分
……………………8分 ……9分
……9分设
 ,
,
因为
 为定值,当
为定值,当 到直线
到直线 的距离
的距离 最大时,△ABP的面积最大,
最大时,△ABP的面积最大, ………………………10分
………………………10分因为
 ,所以当
,所以当 时,
时, max=
max= ,此时
,此时
∴△ABP的面积最大值为
 .……………………………12分
.……………………………12分
练习册系列答案
相关题目
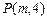 到其准线的距离等于5.
到其准线的距离等于5.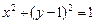 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明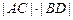 为定值;
为定值;
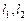 且
且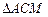 与
与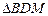 面积之和的最小值.
面积之和的最小值. 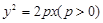 上横坐标是5的点
上横坐标是5的点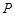 到其焦点
到其焦点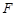 的距离是8,则以
的距离是8,则以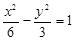 的渐近线相切的圆的方程是
的渐近线相切的圆的方程是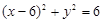
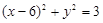
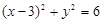
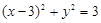
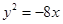 ,动圆恒过点(-2,0)则下列哪条直线是动圆的公切线()
,动圆恒过点(-2,0)则下列哪条直线是动圆的公切线() 的焦点为F,准线为
的焦点为F,准线为 ,点
,点 ,线段
,线段 与抛物线交于点B,过B作
与抛物线交于点B,过B作 ,则
,则 __________
__________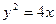 的焦点为F,在第一象限中过抛物线上任意一点P的切线为
的焦点为F,在第一象限中过抛物线上任意一点P的切线为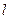 ,过P点作平行于
,过P点作平行于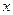 轴的直线
轴的直线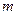 ,过焦点F作平行于
,过焦点F作平行于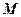 ,若
,若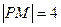 ,则点P的坐标为 .
,则点P的坐标为 .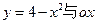 所围成的图形的面积的值是 。
所围成的图形的面积的值是 。 的焦点
的焦点 为
为 ,准线为
,准线为 ,则过点
,则过点 (4,4)且与准线
(4,4)且与准线