题目内容
与y轴相切且和半圆x2+y2=4(0≤x≤2)内切的动圆圆心的轨迹方程是( )A.y2=4(x+1)(0<x≤1)
B.y2=4(x-1)(0<x≤1)
C.y2=-4(x-1)(0<x≤1)
D.y2=-2(x-1)(0<x≤1)
【答案】分析:设出动圆的圆心坐标(x,y),由题意得到关系式 ,整理后即可得到答案.
,整理后即可得到答案.
解答:解:设圆心为(x,y),则动圆的半径为x,
因为与已知圆内且,还要与y轴相切,所以可知x的范围为0<x≤1.
同时原点到动圆圆心的距离为: ,
,
则由题意有下列方程:
 .
.
整理得y2=4-4x(0<x≤1).
所以动圆圆心的轨迹方程为:y2=4-4x(0<x≤1).
故选A.
点评:本题考查了轨迹方程,解答的关键是结合平面几何知识得到动圆圆心所满足的关系式,是中档题.
 ,整理后即可得到答案.
,整理后即可得到答案.解答:解:设圆心为(x,y),则动圆的半径为x,
因为与已知圆内且,还要与y轴相切,所以可知x的范围为0<x≤1.
同时原点到动圆圆心的距离为:
 ,
,则由题意有下列方程:
 .
.整理得y2=4-4x(0<x≤1).
所以动圆圆心的轨迹方程为:y2=4-4x(0<x≤1).
故选A.
点评:本题考查了轨迹方程,解答的关键是结合平面几何知识得到动圆圆心所满足的关系式,是中档题.

练习册系列答案
相关题目
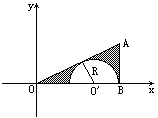
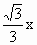 上一点,AB⊥x轴于B,半圆的圆心
上一点,AB⊥x轴于B,半圆的圆心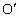 在x轴的正半轴上,且半圆与AB、AO相切,已知△ABO绕x轴旋转一周形成的几何体的体积为
在x轴的正半轴上,且半圆与AB、AO相切,已知△ABO绕x轴旋转一周形成的几何体的体积为 ,求阴影部分旋转成的几何体的体积和表面积.
,求阴影部分旋转成的几何体的体积和表面积.
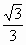 x上一点,AB⊥x轴于B,半圆的圆心
x上一点,AB⊥x轴于B,半圆的圆心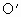 在x轴的正半轴上,且半圆与AB,AO相切,已知△ABO绕x轴旋转一周形成的几何体的体积为9
在x轴的正半轴上,且半圆与AB,AO相切,已知△ABO绕x轴旋转一周形成的几何体的体积为9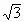 π,求阴影部分旋转成的几何体的体积和表面积.
π,求阴影部分旋转成的几何体的体积和表面积.