题目内容
过点P（2，3）向圆x2+y2=1作两条切线PA、PB，则弦AB所在直线的方程为（ ）
分析：由PA为圆的切线，得到OA与PA垂直，利用勾股定理求出|PA|的长，进而表示出以P为圆心，|PA|为半径的圆方程，根据AB为两圆的公共弦，即可确定出弦AB所在的直线方程．
解答：解：∵PA为圆的切线，∴OA⊥PA，
∴|PA|2=4+9-1=12，
∴以P为圆心，|PA|为半径的圆方程为（x-2）2+（y-3）2=12，
∵AB为两圆的公共弦，
∴弦AB所在的直线方程为[（x-2）2+（y-3）2-12]-（x2+y2-1）=0，
整理得：2x+3y-1=0．
故选B
∴|PA|2=4+9-1=12，
∴以P为圆心，|PA|为半径的圆方程为（x-2）2+（y-3）2=12，
∵AB为两圆的公共弦，
∴弦AB所在的直线方程为[（x-2）2+（y-3）2-12]-（x2+y2-1）=0，
整理得：2x+3y-1=0．
故选B
点评：此题考查了直线与圆的位置关系，表示出以P为圆心，|PA|为半径的圆方程是解本题的关键．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
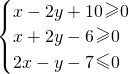内有一个圆，向该区域内随机投点，将点落在圆内的概率最大时的圆记为圆M．
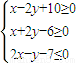内有一个圆，向该区域内随机投点，将点落在圆内的概率最大时的圆记为圆M．