题目内容
已知函数![]()
(1)若![]() 是函数
是函数![]() 的一个极值点,求a的值;
的一个极值点,求a的值;
(2)求证:当![]() 上是增函数;
上是增函数;
(3)若对任意的![]() 成立,求实数m的取值范围。
成立,求实数m的取值范围。
解:
(1)由已知,得![]()
![]()
(2)当![]() 2时,
2时,![]() 0,
0,![]() ,
,
当![]() 时,
时,![]()
![]() ,
,
故![]() 上是增函数。
上是增函数。
(3)当![]()
![]()
于是问题等价于:对任意的![]() ,不等式
,不等式![]() 恒成立。
恒成立。
记![]()
![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在区间(1,2)上递减,
在区间(1,2)上递减,
此时,![]()
故必有m>0,
![]() ,
,
若![]()
![]() 上递减,
上递减,
在此区间上,有![]() 恒成立矛盾,
恒成立矛盾,
故![]() , …………………………………………12分
, …………………………………………12分
这时![]() ,
,
满足题设要求,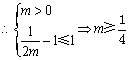
所以,实数m的取值范围为![]()

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目

 是定义域上的单调函数,求
是定义域上的单调函数,求 的取值范围;
的取值范围;
 、
、 ,证明:
,证明:

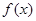 是单调函数,求
是单调函数,求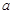 的取值范围;
的取值范围; ,证明:
,证明: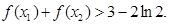

 是定义域上的单调函数,求
是定义域上的单调函数,求 的取值范围;
的取值范围;
 、
、 ,证明:
,证明:

 是
是 的极值点,求
的极值点,求 上的最小值和最大值;
上的最小值和最大值; 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.