题目内容
若x,y满足表达式(x-2)2+y2=1,则 的取值范围是( )
的取值范围是( )A.

B.

C.

D.

【答案】分析:利用图形可求得圆上的点P(x,y)到定点A(4,0)的直线的斜率的范围.
解答: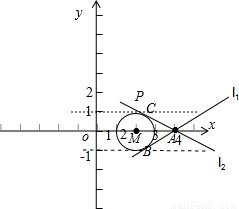 解:∵(x-2)2+y2=1是以M(2,0)为圆心,1为半径的圆的方程,
解:∵(x-2)2+y2=1是以M(2,0)为圆心,1为半径的圆的方程,
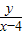 表示该圆上的点P(x,y)到定点A(4,0)的直线的斜率,作图如下:
表示该圆上的点P(x,y)到定点A(4,0)的直线的斜率,作图如下:
由图可知,△AMC与△AMB均为直角三角形,C,D分别为直线PA与该圆的切点,且sin∠CAM=sin∠MAB= ,
,
∴当PA与该圆相切时直线AC的倾斜角α=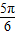 ,直线AB的倾斜角β=
,直线AB的倾斜角β=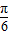 ,
,
又tanα=tan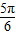 =-
=-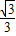 ,tanβ=tan
,tanβ=tan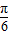 =
=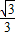 ,当直线PA绕点A逆时针由AC转到AB时,
,当直线PA绕点A逆时针由AC转到AB时,
直线PA的斜率范围为[-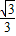 ,
,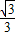 ].
].
故选C.
点评:本题考查直线与圆的位置关系,考查曲线上的点与定点的直线斜率的应用,突出数形结合思想与化归思想的考查,属于中档题.
解答:
 解:∵(x-2)2+y2=1是以M(2,0)为圆心,1为半径的圆的方程,
解:∵(x-2)2+y2=1是以M(2,0)为圆心,1为半径的圆的方程,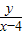 表示该圆上的点P(x,y)到定点A(4,0)的直线的斜率,作图如下:
表示该圆上的点P(x,y)到定点A(4,0)的直线的斜率,作图如下:由图可知,△AMC与△AMB均为直角三角形,C,D分别为直线PA与该圆的切点,且sin∠CAM=sin∠MAB=
 ,
,∴当PA与该圆相切时直线AC的倾斜角α=
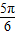 ,直线AB的倾斜角β=
,直线AB的倾斜角β=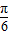 ,
,又tanα=tan
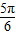 =-
=-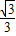 ,tanβ=tan
,tanβ=tan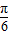 =
=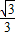 ,当直线PA绕点A逆时针由AC转到AB时,
,当直线PA绕点A逆时针由AC转到AB时,直线PA的斜率范围为[-
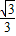 ,
,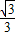 ].
].故选C.
点评:本题考查直线与圆的位置关系,考查曲线上的点与定点的直线斜率的应用,突出数形结合思想与化归思想的考查,属于中档题.

练习册系列答案
相关题目
 一化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t、硝酸盐18t;生产1车皮乙种肥料的主要原料是磷酸盐1t、硝酸盐15t.现库存磷酸盐10t、硝酸盐66t.若生产1车皮甲种肥料产生的利润为10000元;生产1车皮乙种肥料产生的利润为5000元.
一化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t、硝酸盐18t;生产1车皮乙种肥料的主要原料是磷酸盐1t、硝酸盐15t.现库存磷酸盐10t、硝酸盐66t.若生产1车皮甲种肥料产生的利润为10000元;生产1车皮乙种肥料产生的利润为5000元. ,对任意实数x,y满足:f(x+y)=f(x)+f(y)-3.
,对任意实数x,y满足:f(x+y)=f(x)+f(y)-3. ,求bn;
,求bn; ,试证c1+c2+…+c2010<89.
,试证c1+c2+…+c2010<89.