题目内容
已知正实数m、n满足 ,当mn取得最小值时,椭圆
,当mn取得最小值时,椭圆 的离心率为( )
的离心率为( )A.

B.

C.

D.

【答案】分析:先利用基本不等式求出当m•n取得最小值时m和n 的值,从而得到椭圆的标准方程,由方程求得椭圆的离心率.
解答:解:∵已知 ,则 1≥2
,则 1≥2  ,∴mn≥6,当且仅当 m=2,n=3时,等号成立.
,∴mn≥6,当且仅当 m=2,n=3时,等号成立.
此时,椭圆的方程为 +
+ =1,b=
=1,b= ,a=
,a= ,c=1,∴e=
,c=1,∴e= =
= ,
,
故选C.
点评:本题考查基本不等式的应用,椭圆的简单性质的应用.
解答:解:∵已知
 ,则 1≥2
,则 1≥2  ,∴mn≥6,当且仅当 m=2,n=3时,等号成立.
,∴mn≥6,当且仅当 m=2,n=3时,等号成立.此时,椭圆的方程为
 +
+ =1,b=
=1,b= ,a=
,a= ,c=1,∴e=
,c=1,∴e= =
= ,
,故选C.
点评:本题考查基本不等式的应用,椭圆的简单性质的应用.

练习册系列答案
相关题目
已知正实数m、n满足
+
=1,当mn取得最小值时,椭圆
+
=1的离心率为( )
| 1 |
| m |
| 3 |
| 2n |
| x2 |
| m |
| y2 |
| n |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 ,当mn取得最小值时,椭圆
,当mn取得最小值时,椭圆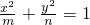 的离心率为
的离心率为


