题目内容
(本题满分12分)
在△ABC中,三个内角是A、B、C的对边分别是a、b、c,其中c=10,且
 (I)求证:△ABC是直角三角形;
(I)求证:△ABC是直角三角形;
(II)设圆O过A、B、C三点,点P位于劣弧AC上,∠PAB=60°.求四边形ABCP的面积.
在△ABC中,三个内角是A、B、C的对边分别是a、b、c,其中c=10,且

 (I)求证:△ABC是直角三角形;
(I)求证:△ABC是直角三角形;(II)设圆O过A、B、C三点,点P位于劣弧AC上,∠PAB=60°.求四边形ABCP的面积.
(1)略
(2)18+
 .
.(1)证明:根据正弦定理得, …………2分
…………2分
整理为,sinAcosA=sinBcosB,即sin2A=sin2B.
∵sin2A-sin2B=0, ∴2cos(A+B)·sin(A-B)=0.
∵A+B=π-C, ∴cosC·sin(A-B)=0.…………5分
 ∴
∴ …………7分
…………7分
 ∴舍去A=" " B. ∴
∴舍去A=" " B. ∴ .
.
故△ABC是直角三角形.………………8分
(2)解:由(1)可得:a=6,b=8.
在Rt△ACB中, ∴
∴
=
= …………11分
…………11分
连结PB,在Rt△APB中,AP=AB·cos∠PAB=5,
∴四边形ABCP的面积 =24+
=24+
=18+ .………………14分
.………………14分
 …………2分
…………2分整理为,sinAcosA=sinBcosB,即sin2A=sin2B.
∵sin2A-sin2B=0, ∴2cos(A+B)·sin(A-B)=0.
∵A+B=π-C, ∴cosC·sin(A-B)=0.…………5分
 ∴
∴ …………7分
…………7分 ∴舍去A=" " B. ∴
∴舍去A=" " B. ∴ .
.故△ABC是直角三角形.………………8分
(2)解:由(1)可得:a=6,b=8.
|
 ∴
∴
=

=
 …………11分
…………11分连结PB,在Rt△APB中,AP=AB·cos∠PAB=5,
|
 =24+
=24+
=18+
 .………………14分
.………………14分
练习册系列答案
相关题目


 .
. 化简成
化简成 的形式(6分);
的形式(6分); ,求边AC的长. (7分);
,求边AC的长. (7分);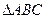 的内角A、B、C所对的边分别为
的内角A、B、C所对的边分别为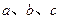 ,若
,若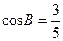
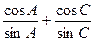 的值;
的值;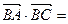 3,求
3,求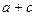 的值。
的值。 ,且满足
,且满足 .
. =
= .
. ,且sin2 A+sin2B=
,且sin2 A+sin2B= sin2 C,
sin2 C, 中,若
中,若 ,则角C的大小为
,则角C的大小为



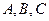 三点在曲线
三点在曲线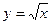 上,其横坐标依次为
上,其横坐标依次为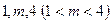 ,当
,当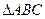 的面积最大时,
的面积最大时,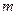 的值等于( )
的值等于( )



 的内角
的内角 的对边分别为
的对边分别为 。若
。若 ,则
,则 等于()
等于()



 中,边
中,边 所对的角分别为A,B,C,
所对的角分别为A,B,C,  ,则
,则 =( )
=( )