题目内容
为了研究某种细菌随时间x变化繁殖的个数，收集数据如下：天数x/天 | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖个数y/个 | 6 | 12 | 25 | 49 | 95 | 190 |
（1）作出y关于x的散点图.
（2）写出y关于x的模拟函数.
解:(1)作散点图.
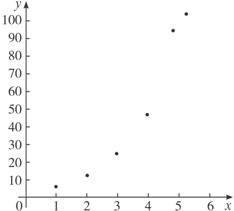
(2)由散点图知x、y之间满足函数关系为y=ae bx.
设μ=lny,c=lna,则μ=c+bx.
x | 1 | 2 | 3 | 4 | 5 | 6 |
μ | 1.791 8 | 2.484 9 | 3.218 9 | 3.891 8 | 4.553 9 | 5.247 0 |
=21,
=21.188 3,
2=91,
μi=86.237,
=3.5,
=3.531 4,
b=
=
=
=0.69,
c=
-b
=3.531 4-0.69×3.5=1.115 9,
∴c =1.115 9+0.69x.∴y=e1.115 9·e0.69x.
练习册系列答案
相关题目
为了研究某种细菌随时间x变化，繁殖的个数，收集数据如下：
| 天数x/天 | 1 | 2 | 3 | 4 | 5 | 6 |
| 繁殖个数y/个 | 6 | 12 | 25 | 49 | 95 | 190 |
(1) 用天数作解释变量，繁殖个数作预报变量，作出这些数据的散点图
(2) 求出回归方程
(3) 描述解释变量与预报变量之间的关系，计算残差、相关指数R2.
为了研究某种细菌随时间x的变化,繁殖的个数，收集数据如下：
天数x/天 | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖个数Y/个 | 6 | 12 | 25 | 49 | 95 | 190 |
（1）用天数作为解释变量，繁殖个数作为预报变量，作出这些数据的散点图;
（2）描述解释变量与预报变量之间的关系;
（3）计算残差、相关指数R2.
为了研究某种细菌随时间x变化繁殖的个数,收集数据如下:
天数(x/天) | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖个数(y/个) | 6 | 12 | 25 | 49 | 95 | 190 |
(1)用天数作为解释变量,繁殖个数作为预报变量,作出这些数据的散点图;
(2)描述解释变量与预报变量之间的关系;
(3)计算残差、相关指数R2.