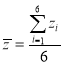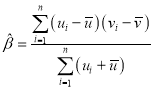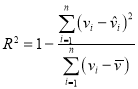题目内容
【题目】设曲线![]()
![]() ,点
,点![]() 为
为![]() 的焦点,过点
的焦点,过点![]() 作斜率为1的直线
作斜率为1的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() ,
,![]() 的横坐标的倒数和为-1.
的横坐标的倒数和为-1.
(1)求曲线![]() 的标准方程;
的标准方程;
(2)过焦点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,分别以点
两点,分别以点![]() ,
,![]() 为切点作曲线
为切点作曲线![]() 的切线相交于点
的切线相交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 轴于点
轴于点![]() ,求三角形
,求三角形![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() ;(2)2.
;(2)2.
【解析】
(1)设直线![]() 的方程,与抛物线联立,由点
的方程,与抛物线联立,由点![]() ,
,![]() 的横坐标的倒数和为-1,结合韦达定理代入求值即可;(2)设
的横坐标的倒数和为-1,结合韦达定理代入求值即可;(2)设![]() 的方程为
的方程为![]() ,与抛物线联立求得
,与抛物线联立求得![]() ,求过M,N的切线方程求得Q(2k,0),利用点到线的距离求点
,求过M,N的切线方程求得Q(2k,0),利用点到线的距离求点![]() 到直线/的距离为
到直线/的距离为![]() ,利用
,利用![]() 求解即可
求解即可
(1)由题意可知:![]() ,故可设直线
,故可设直线![]() 的方程为
的方程为![]() 即
即![]()
联立方程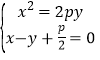 可得
可得![]() ∴
∴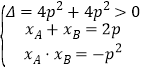
由题意知:![]() ,即
,即![]() ,即
,即![]() ,得
,得![]() .
.
∴曲线![]() 的标准方程为
的标准方程为![]() .
.
(2)由题意知直线![]() 的斜率是存在的,故设
的斜率是存在的,故设![]() 的方程为
的方程为![]() ,
,
设![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,
,![]()
![]()
联立方程![]() 可得
可得![]() ∴
∴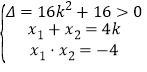
∴![]() .
.
由![]() ,得
,得![]() . ∴
. ∴![]() .
.
∴![]() ,∴
,∴![]() ……①
……①
∴![]() ,∴
,∴![]() ……②
……②
上述两式相减得:![]() ,∴
,∴![]() .∴点
.∴点![]() 坐标为
坐标为![]() .
.
∴点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
∴![]()
又∵![]() ,∴
,∴![]() .易知当
.易知当![]() 时,
时,![]() 的面积最小,且为2,
的面积最小,且为2,
即![]() .
.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目