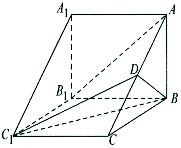
题目内容
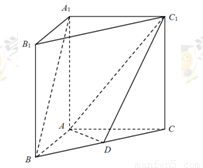
直三棱柱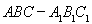 中,
中,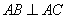 ,
,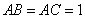 ,
,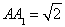 ,D为BC中点.
,D为BC中点.
(Ⅰ)求证: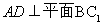 ;
;
(Ⅱ)求证: ;
;
(Ⅲ)求二面角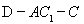 的正弦值.
的正弦值.
【答案】
(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)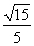
【解析】
试题分析:(Ⅰ)由等腰三角形底边中线即为高线可得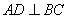 ,由三棱柱为直棱柱可得侧棱垂直底面从而垂直底面内的任意一条直线,即可得
,由三棱柱为直棱柱可得侧棱垂直底面从而垂直底面内的任意一条直线,即可得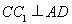 ,根据线面垂直的判定定理可得
,根据线面垂直的判定定理可得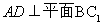 。(Ⅱ)连接
。(Ⅱ)连接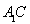 交
交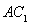 于
于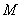 ,连接
,连接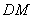 。可知
。可知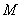 为
为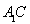 中点。由三角形中位线可证得
中点。由三角形中位线可证得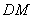 //
//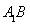 ,再根据线面平行的性质定理可得
,再根据线面平行的性质定理可得 。(Ⅲ)建立空间坐标系,根据各边长可得各点的坐标,从而可求出面
。(Ⅲ)建立空间坐标系,根据各边长可得各点的坐标,从而可求出面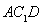 的法向量。由题意可证得
的法向量。由题意可证得 ,所以
,所以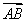 即为面
即为面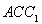 的一个法向量。可用向量数量积公式求两法向量所成角的余弦值。但两法向量所成的角与二面角相等或互补,需根据题意判断。
的一个法向量。可用向量数量积公式求两法向量所成角的余弦值。但两法向量所成的角与二面角相等或互补,需根据题意判断。
试题解析:(Ⅰ) 因为 三棱柱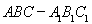 中,
中,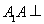 平面
平面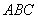 ,所以
,所以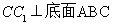
所以CC1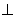 AD 1分
AD 1分
 AB=AC,且D为AC中点
AB=AC,且D为AC中点
 AD
AD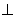 BC 2分
BC 2分

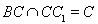 3分
3分
 AD
AD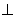 平面BC1 4分
平面BC1 4分
(Ⅱ)
连接A1C交AC1于M,连接DM
 侧面AC1为平行四边形
侧面AC1为平行四边形
 M为A1C中点 5分
M为A1C中点 5分
 D为BC中点
D为BC中点
 DM//A1B 6分
DM//A1B 6分

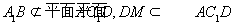 7分
7分
 A1B//平面AC1D 8分
A1B//平面AC1D 8分
(Ⅲ) 在直三棱柱
在直三棱柱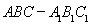 中,AA1
中,AA1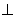 平面ABC
平面ABC
 AA1
AA1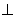 AB,AA1
AB,AA1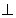 AC
AC
又 AB
AB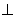 AC 9分
AC 9分
 以A为坐标原点,AB为Ox轴,AC为Oy轴,AA1为Oz轴建立空间直角坐标系
以A为坐标原点,AB为Ox轴,AC为Oy轴,AA1为Oz轴建立空间直角坐标系
则A(0,0,0),B(1,0,0),C(0,1,0),D(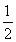 ,
,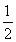 ,0),C1(0,1,
,0),C1(0,1,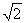 ),
),
A1(0,0,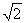 ),
),
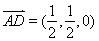 ,
,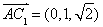 10分
10分
设平面AC1D的法向量为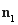 =(x,y,z),
=(x,y,z),




令z=1,则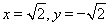

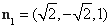 11分
11分
又 AB
AB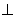 平面AC1
平面AC1
 平面AC1的法向量
平面AC1的法向量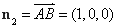 12分
12分
若二面角D-AC1-C的大小为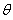
因为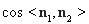
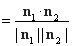
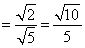 13分
13分
又 由图可知二面角D-AC1-C为锐角,
二面角的余弦值为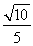
即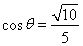 ,
,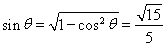 。 14分
。 14分
考点:线线垂直、线面垂直、线面平行,二面角。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
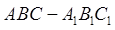 中,
中,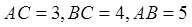 ,
,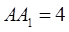 ,点D是AB的中点.
,点D是AB的中点.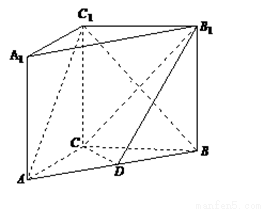
 ;
;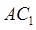 ∥平面
∥平面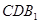 ;
;  与
与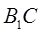 所成角的余弦值.
所成角的余弦值.  中,AB⊥BC,D为AC的中点,
中,AB⊥BC,D为AC的中点, 。
。 ∥平面
∥平面 ;
; 的体积为2,求二面角
的体积为2,求二面角 的正切值。
的正切值。
 (三条侧棱和底面均垂直的三棱柱叫做直三棱柱)中,若
(三条侧棱和底面均垂直的三棱柱叫做直三棱柱)中,若 ,
, ,则异面直线
,则异面直线 与
与 所成的角等于
( )
所成的角等于
( ) 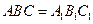 中,AB⊥BC,D为AC的中点,
中,AB⊥BC,D为AC的中点,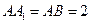 。
。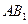 ∥平面
∥平面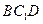 ;
;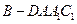 的体积为2,求二面角
的体积为2,求二面角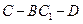 的正切值。
的正切值。