题目内容
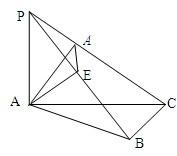
如图，PA⊥△ABC所在平面，AB=AC=13，BC=10，PA=5，求点P到直线BC的距离．
解：取BC的中点D，连接AD、PD
∵AB=AC=13，
∴AD⊥BC
而PA⊥△ABC所在平面，BC?平面ABC
∴PA⊥BC
而AD∩PA=A
∴BC⊥面PAD，PD?平面ABC
∴BC⊥PD
即PD为P到直线BC的距离
AD=12，PA=5，在直角三角形PAD中，AD=13
∴P到直线BC的距离为13
分析：取BC的中点D，连接AD、PD，根据等腰三角形可知AD⊥BC，而PA⊥BC，AD∩PA=A满足线面垂直的判定定理可知BC⊥面PAD，根据线面垂直的性质可知BC⊥PD，则PD为P到直线BC的距离．在直角三角形PAD中求出AD即可．
点评：本题主要考查了点到直线的距离，以及线面垂直的判定定理和性质，同时考查了空间想象能力和计算能力，属于基础题．
∵AB=AC=13，
∴AD⊥BC
而PA⊥△ABC所在平面，BC?平面ABC
∴PA⊥BC
而AD∩PA=A
∴BC⊥面PAD，PD?平面ABC
∴BC⊥PD
即PD为P到直线BC的距离
AD=12，PA=5，在直角三角形PAD中，AD=13
∴P到直线BC的距离为13
分析：取BC的中点D，连接AD、PD，根据等腰三角形可知AD⊥BC，而PA⊥BC，AD∩PA=A满足线面垂直的判定定理可知BC⊥面PAD，根据线面垂直的性质可知BC⊥PD，则PD为P到直线BC的距离．在直角三角形PAD中求出AD即可．
点评：本题主要考查了点到直线的距离，以及线面垂直的判定定理和性质，同时考查了空间想象能力和计算能力，属于基础题．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
如图，在△ABC中，∠B=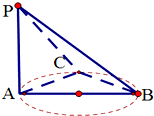
如图，PA⊥平面ABC，AB是圆的直径，C是圆上的任意点（不同于A，B），则图中互相垂直的平面共有（ ）
如图，PA⊥△ABC所在平面，AB=AC=13，BC=10，PA=5，求点P到直线BC的距离．