题目内容
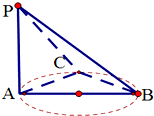如图，PA⊥平面ABC，AB是圆的直径，C是圆上的任意点（不同于A，B），则图中互相垂直的平面共有（ ）分析：由已知中已知PA⊥平面BCA，AC⊥CB，结合线面垂直及面面垂直的判定定理，对三棱锥的四个平面：平面ABC，平面ABP，平面PCB和平面ACP之间的关系逐一进行判断，即可得到结论．
解答：解：如下图所示
因为PA⊥平面ACB，PA?平面PAC，所以平面PAC⊥平面ACB，
平面PAB⊥平面ACB，
因为PA⊥平面ACB，CB?平面ACB，所以PA⊥CB；
又AC⊥CB，且PA∩AC=A，所以CB⊥平面PAC．
又CB?平面PCB，所以平面PAC⊥平面PCB．
共有：平面PAC⊥平面ACB；平面PAB⊥平面ACB；平面PAC⊥平面PCB．
故选B．
因为PA⊥平面ACB，PA?平面PAC，所以平面PAC⊥平面ACB，
平面PAB⊥平面ACB，
因为PA⊥平面ACB，CB?平面ACB，所以PA⊥CB；
又AC⊥CB，且PA∩AC=A，所以CB⊥平面PAC．
又CB?平面PCB，所以平面PAC⊥平面PCB．
共有：平面PAC⊥平面ACB；平面PAB⊥平面ACB；平面PAC⊥平面PCB．
故选B．
点评：本题考查的知识点是平面与平面垂直的判定，其中熟练掌握线面垂直及面面垂直的判定定理是解答本题的关键．
练习册系列答案
走进文言文系列答案
相关题目
如图，PA⊥平面ABCD，四边形ABCD是正方形，PA=AD=2，M，N分别是AB，PC的中点．
如图，PA⊥平面AC，四边形ABCD是矩形，E、F分别是AB、PD的中点．
如图，PA⊥平面ABC，AC⊥BC，AB=2，
（2010•天津模拟）如图，PA⊥平面ABCD，ABCD是矩形，PA=AB=1，PD与平面ABCD所成的角是30°，点
如图，PA⊥平面ABCD，四边形ABCD是矩形，PA=AB=1，PD与平面ABCD所成的角是30°，点F是PB的中点，点E在边BC上移动．