Question

20、如图，PA⊥平面ABC，AE⊥PB，AB⊥BC，AF⊥PC，垂足分别为B、E、F；求证：EF⊥PC．

Answer 1

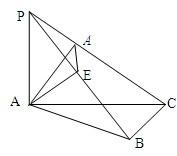
分析：欲证EF⊥PC，可先证PC⊥平面AEF，根据直线与平面垂直的判定定理可知只需证PC与平面AEF内两相交直线垂直，根据PA⊥平面ABC则PA⊥BC，而AB⊥BC，则BC⊥平面PAB又AE?平面PAB，根据线面垂直的性质可知AE⊥BC，同理AE⊥PC，而AF⊥PC，满足定理所需条件．

解答：证明：∵PA⊥平面ABC，∴PA⊥BC，∵AB⊥BC，
∴BC⊥平面PAB，∵AE?平面PAB，∴AE⊥BC，
∵AE⊥PB，∴AE⊥平面PBC，∴AE⊥PC，
∵AF⊥PC，∴PC⊥平面AEF，
∴EF⊥PC．

点评：本小题主要考查直线与平面垂直的判定，以及线面垂直的性质等基础知识，考查空间想象能力、化归与转化思想，属于基础题．