题目内容
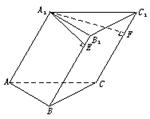
如图,已知三棱柱A1B1C1—ABC的底面是边长为2的正三角形,侧棱A1A与AB、AC均成45°角,且A1E⊥B1B于E,A1F⊥CC1于F.
(1)求点A到平面B1BCC1的距离;
(2)当AA1多长时,点A1到平面ABC与平面B1BCC1的距离相等.
(1)所求距离为2 (2)当AA1=![]() 时满足条件.
时满足条件.
解析:
(1)∵BB1⊥A1E,CC1⊥A1F,BB1∥CC1
∴BB1⊥平面A1EF
即面A1EF⊥面BB1C1C
在Rt△A1EB1中,
∵∠A1B1E=45°,A1B1=a
∴A1E=![]() a,同理A1F=
a,同理A1F=![]() a,又EF=a,∴A1E=
a,又EF=a,∴A1E=![]() a
a
同理A1F=![]() a,又EF=a
a,又EF=a
∴△EA1F为等腰直角三角形,∠EA1F=90°
过A1作A1N⊥EF,则N为EF中点,且A1N⊥平面BCC1B1
即A1N为点A1到平面BCC1B1的距离
∴A1N=![]()
又∵AA1∥面BCC1B,A到平面BCC1B1的距离为![]()
∴a=2,∴所求距离为2
(2)设BC、B1C1的中点分别为D、D1,连结AD、DD1和A1D1,则DD1必过点N,易证ADD1A1为平行四边形.
∵B1C1⊥D1D,B1C1⊥A1N
∴B1C1⊥平面ADD1A1
∴BC⊥平面ADD1A1
得平面ABC⊥平面ADD1A1,过A1作A1M⊥平面ABC,交AD于M,
若A1M=A1N,又∠A1AM=∠A1D1N,∠AMA1=∠A1ND1=90°
∴△AMA1≌△A1ND1,∴AA1=A1D1=![]() ,即当AA1=
,即当AA1=![]() 时满足条件.
时满足条件.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
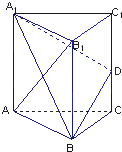 如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱C C1到点A1的最短路线长为2
如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱C C1到点A1的最短路线长为2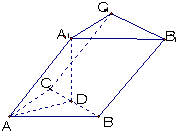 如图,已知三棱柱ABC-A1B1C1的侧棱长与底面边长都等于1,A1在底面ABC上的射影D为BC的中点,则侧棱AA1与底面ABC所成角的大小为
如图,已知三棱柱ABC-A1B1C1的侧棱长与底面边长都等于1,A1在底面ABC上的射影D为BC的中点,则侧棱AA1与底面ABC所成角的大小为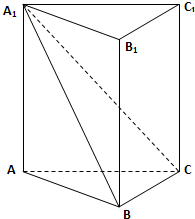 如图,已知三棱柱ABC-A1B1C1中,侧棱A A1⊥底面ABC,AB⊥BC;
如图,已知三棱柱ABC-A1B1C1中,侧棱A A1⊥底面ABC,AB⊥BC;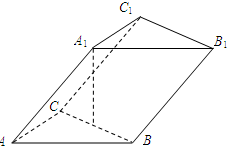 如图:已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等,过顶点A1作底面ABC的垂线,若垂足为BC的中点,则异面直线AB与CC1成的角的余弦值为
如图:已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等,过顶点A1作底面ABC的垂线,若垂足为BC的中点,则异面直线AB与CC1成的角的余弦值为 如图,已知三棱柱ABC-A1B1C1的侧棱与底面所成的角为60°,AB=BC,A1A=A1C=2,AB⊥BC,侧面AA1C1C⊥底面ABC.
如图,已知三棱柱ABC-A1B1C1的侧棱与底面所成的角为60°,AB=BC,A1A=A1C=2,AB⊥BC,侧面AA1C1C⊥底面ABC.