题目内容
若直线2ax-by+2=0(a>0,b>0)始终平分圆x2+y2+2x-4y+1=0的周长,则ab的最大值是( )
| A. 4 | B. 2 | C. | D. |
C
分析:把圆的方程化为标准形式,求出圆心和半径,把圆心坐标代入直线2ax-by+2=0,利用基本不等式求出ab的最大值.
解答:解:圆x2+y2+2x-4y+1="0" 即 (x+1)2 +(y-2)2=4,表示圆心在(-1,2),半径等于2的圆,
由题意知,圆心(-1,2)在直线2ax-by+2=0(a>0,b>0)上,
∴-2a-2b+2=0.
再由 a+b=1≥2 ,∴1≥4ab,ab≤
,∴1≥4ab,ab≤ ,
,
故ab的最大值是 故选 C.
故选 C.
解答:解:圆x2+y2+2x-4y+1="0" 即 (x+1)2 +(y-2)2=4,表示圆心在(-1,2),半径等于2的圆,
由题意知,圆心(-1,2)在直线2ax-by+2=0(a>0,b>0)上,
∴-2a-2b+2=0.
再由 a+b=1≥2
 ,∴1≥4ab,ab≤
,∴1≥4ab,ab≤ ,
,故ab的最大值是
 故选 C.
故选 C.
练习册系列答案
相关题目
 的交点且垂直于直线
的交点且垂直于直线 的直线方程.
的直线方程.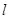 经过两条直线
经过两条直线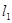 :
: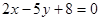 和
和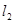
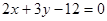 的交点,且分这两条直线与
的交点,且分这两条直线与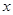 轴围成的三角形面积为
轴围成的三角形面积为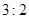 两部分,求直线
两部分,求直线 ,
, ,若
,若 ∥
∥ ,则
,则 的值是( )
的值是( ) 

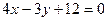 在
在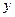 轴上的截距是 ( )
轴上的截距是 ( )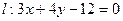 与
与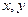 轴的正半轴分别交于
轴的正半轴分别交于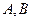 两点,直线
两点,直线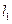 和
和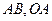 分别交于
分别交于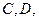 且平分△
且平分△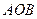 的面积,求
的面积,求 的最小值.
的最小值.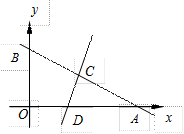
 与L2:
与L2: 互相垂直,则
互相垂直,则 的值为______
的值为______