题目内容
5. 如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为$\frac{4}{3}$.
如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为$\frac{4}{3}$.
分析 首先连接BD,由在菱形ABCD中,AB=4cm,∠ADC=120°,可得△ABD是等边三角形,又由△DEF为等边三角形,可得△ADE≌△BDF(SAS),继而可得当AE=BF时,△DEF是等边三角形,即可求得答案.
解答 解:连接BD,,点e的速度为1cm-s,点f的速度为 - 初中数学 - 菁优网.mht!http://img.jyeoo.net/quiz/images/201506/179/be766462.png)
∵在菱形ABCD中,∠ADC=120°,
∴AD=AB,∠A=60°,∠ADB=$\frac{1}{2}$∠ADC=60°,
∴△ABD是等边三角形,
∴BD=AD,
∵若△DEF是等边三角形,则∠DEF=60°,DE=DF,
∴∠ADE=∠BDF,
在△ADE和△BDF中,
$\left\{\begin{array}{l}AD=BD\\∠ADE=∠BDF\\ DE=DF\end{array}\right.$,
∴△ADE≌△BDF(SAS),
∴AE=BF,
∴当AE=BF时,△DEF是等边三角形,
∵E的速度为1cm/s,点F的速度为2cm/s,
∴AE=tcm,CF=2tcm,
则BF=BC-CF=4-2t(cm),
∴t=4-2t,
解得:t=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查了菱形的性质、全等三角形的判定与性质以及等边三角形的判定与性质.注意证得△ABD是等边三角形且△ADE≌△BDF是关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
20.已知α,β为锐角三角形的两个锐角,则以下结论正确的是( )
| A. | sinα<sinβ | B. | cosα<sinβ | C. | cosα<cosβ | D. | cosα>cosβ |
10.下列说法正确的有( )
①方向相同的向量叫相等向量;
②零向量的长度为0;
③共线向量是在同一条直线上的向量;
④零向量是没有方向的向量;
⑤共线向量不一定相等;
⑥平行向量方向相同.
①方向相同的向量叫相等向量;
②零向量的长度为0;
③共线向量是在同一条直线上的向量;
④零向量是没有方向的向量;
⑤共线向量不一定相等;
⑥平行向量方向相同.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
15.已知复数Z=(1+i)(2+i607)的实部是m,虚部是n,则mn=( )
| A. | 3 | B. | -3 | C. | 3i | D. | -3i |
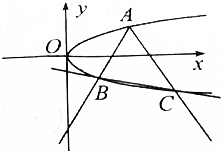 如图,过抛物线y2=x上一点A(4,2)作倾斜角互补的两条直线AB,AC,交抛物线于B,C两点,求证:直线BC的斜率是定值.
如图,过抛物线y2=x上一点A(4,2)作倾斜角互补的两条直线AB,AC,交抛物线于B,C两点,求证:直线BC的斜率是定值.