题目内容
某生产厂商更新设备，已知在未来x 年内，此设备所花费的各种费用总和y（万元）与x
满足函数关系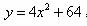
，若欲使此设备的年平均花费最低，则此设备的使用年限x为
（ ）
A．3 B．4 C．5 D．6
B
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
导学教程高中新课标系列答案小学课时特训系列答案题目内容
某生产厂商更新设备，已知在未来x 年内，此设备所花费的各种费用总和y（万元）与x
满足函数关系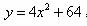，若欲使此设备的年平均花费最低，则此设备的使用年限x为
（ ）
A．3 B．4 C．5 D．6
B
导学教程高中新课标系列答案小学课时特训系列答案
等于（ ）
，
是一个矩形花坛，其中
米，
米．现将矩形花坛
，要求：
在
上，
在
上，对角线
过
点，且矩形
米，矩形
平方米，试用解析式将
的值．
的离心率为 ；渐近线的方程为 ．
于点E ，将△ADE沿DE
的位置，使
，如图 2．
平面BCDE ；
的余弦值；
？若存在，求出
的
被直线
分成两个区域
（包括边界），
，则圆心C到抛物线上任意一点距离的最小值是__________；
内（包括边界）且与三侧边界均有公共点，则圆C的半径是__________.
上一点
处的切线方程是 .