题目内容
已知点A(0,-3),O为坐标原点,动点P(x,y)满足|PA|=2|PO|.
(1)求动点P的轨迹方程;
(2)若关于直线y=k(x-1)对称的两点M,N在动点P的轨迹上,且直线MN与x2+y2=1相切,试求直线MN的方程.
(1)求动点P的轨迹方程;
(2)若关于直线y=k(x-1)对称的两点M,N在动点P的轨迹上,且直线MN与x2+y2=1相切,试求直线MN的方程.
分析:(1)设点P的坐标为(x,y),进而表示出|PA|和|PO|,根据|PA|=2|PO|,求得点P的轨迹方程;
(2)设出与直线y=k(x-1)垂直的直线方程为y=-
x+b,和x2+y2-2y-3=0联立后利用根与系数关系得到M,N的横纵坐标的和,求得M,N的中点坐标,代入直线y=k(x-1)求k值,再由直线MN和圆相切求b,则答案可求.
(2)设出与直线y=k(x-1)垂直的直线方程为y=-
| 1 |
| k |
解答:解:(1)设P(x,y),则|PA|=
,|PO|=
.
由|PA|=2|PO|,得
=2
.
整理得:x2+y2-2y-3=0;
(2)设与直线y=k(x-1)垂直的直线方程为y=-
x+b,即x+ky-kb=0.
联立
,得(1+
)x2-
(b+1)x+b2-2b-3=0.
设M(x1,y1),N(x2,y2),
则x1+x2=
,x1x2=
.
∴y1+y2=-
(x1+x2)+2b=-
•
+2b=
.
∵两点M,N关于直线y=k(x-1)对称,
∴
=k(
-1),整理得:k3-k2+k-1=0,解得k=1.
∴与直线y=k(x-1)垂直的直线方程为x+y-b=0.
又直线MN与x2+y2=1相切,
∴
=1,解得b=±
.
∴直线MN的方程为x-y±
=0.
| x2+(y+3)2 |
| x2+y2 |
由|PA|=2|PO|,得
| x2+(y+3)2 |
| x2+y2 |
整理得:x2+y2-2y-3=0;
(2)设与直线y=k(x-1)垂直的直线方程为y=-
| 1 |
| k |
联立
|
| 1 |
| k2 |
| 2 |
| k |
设M(x1,y1),N(x2,y2),
则x1+x2=
| 2k(b+1) |
| k2+1 |
| k2(b2-2b-3) |
| k2+1 |
∴y1+y2=-
| 1 |
| k |
| 1 |
| k |
| 2k(b+1) |
| k2+1 |
| 2k2b-2 |
| k2+1 |
∵两点M,N关于直线y=k(x-1)对称,
∴
| k2b-1 |
| k2+1 |
| kb+k |
| k2+1 |
∴与直线y=k(x-1)垂直的直线方程为x+y-b=0.
又直线MN与x2+y2=1相切,
∴
| |-b| | ||
|
| 2 |
∴直线MN的方程为x-y±
| 2 |
点评:本题考查了轨迹方程,考查了直线与圆锥曲线的关系,解答此类问题常采用“设而不求”的解题思想方法,即利用直线和圆锥曲线的关系联立方程组,化为关于x(或y)的方程后利用根与系数的关系解题,考查了学生的计算能力,在高考试题中往往以压轴题的形式出现.

练习册系列答案
相关题目
 如图,已知点A(0,-3),动点P满足|PA|=2|PO|,其中O为坐标原点.
如图,已知点A(0,-3),动点P满足|PA|=2|PO|,其中O为坐标原点.
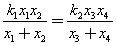 ;
;