题目内容
设不等式(2x-1)>m(x2-1)对满足|m|≤2的一切实数m的值都成立,求x的取值范围.
解:①若x2-1=0,即x=±1,且2x-1>0,即x>![]() 时,此时x=1,原不等式对
时,此时x=1,原不等式对
|m|≤2恒成立;
②若x2-1>0,要使![]() >m,对|m|≤2恒成立,只要
>m,对|m|≤2恒成立,只要![]() >2, 即
>2, 即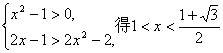 ;
;
③若x2-1<0时,要使![]() <m,对|m|≤2恒成立,只要
<m,对|m|≤2恒成立,只要![]() <-2,即
<-2,即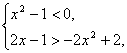
得![]() <x<1.
<x<1.
综合①②③得,所求x的范围为
![]()

练习册系列答案
相关题目
题目内容
设不等式(2x-1)>m(x2-1)对满足|m|≤2的一切实数m的值都成立,求x的取值范围.
解:①若x2-1=0,即x=±1,且2x-1>0,即x>![]() 时,此时x=1,原不等式对
时,此时x=1,原不等式对
|m|≤2恒成立;
②若x2-1>0,要使![]() >m,对|m|≤2恒成立,只要
>m,对|m|≤2恒成立,只要![]() >2, 即
>2, 即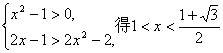 ;
;
③若x2-1<0时,要使![]() <m,对|m|≤2恒成立,只要
<m,对|m|≤2恒成立,只要![]() <-2,即
<-2,即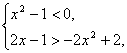
得![]() <x<1.
<x<1.
综合①②③得,所求x的范围为
![]()
