题目内容
已知函数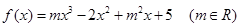 且
且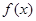 在
在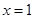 处取得极小值
处取得极小值
(1)求m的值。
(2)若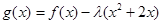 在
在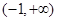 上是增函数,求实数
上是增函数,求实数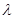 的取值范围。
的取值范围。
【答案】
(1)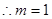 (2)
(2)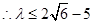
【解析】(1)对函数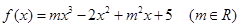 求导,当
求导,当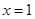 时,令导函数为0,求出
时,令导函数为0,求出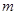 的值,要代入到原函数中进行验证,保证在
的值,要代入到原函数中进行验证,保证在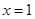 处取得极小值,因为导函数为0的值并不一定取得极值;(2)函数
处取得极小值,因为导函数为0的值并不一定取得极值;(2)函数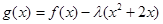 在
在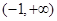 上是增函数,就是
上是增函数,就是
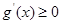 在
在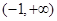 上恒成立,把
上恒成立,把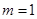 代入分离参数整理得
代入分离参数整理得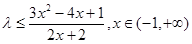 恒成立,只需
恒成立,只需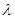 小于等于右边的最小值,利用不等式求出
小于等于右边的最小值,利用不等式求出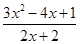 在
在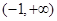 上的最小值,即得
上的最小值,即得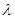 的范围。
的范围。
(1)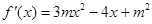
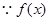 在
在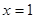 处取得极小值
处取得极小值
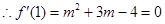 得
得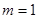 或
或
当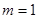 时
时 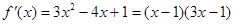
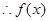 在
在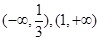 上是增函数在
上是增函数在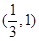 上是减函数
上是减函数
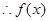 在
在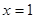 处取得极小值
处取得极小值
当 时
时 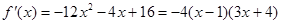
在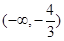
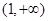 上是减函数
在
上是减函数
在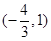 上是增函数
上是增函数
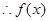 在
在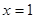 处取得极大值极大值
,不符题意
处取得极大值极大值
,不符题意
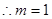 (6分)
(6分)
(2)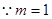
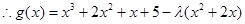
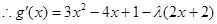
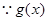 在
在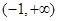 上是增函数,
上是增函数,
 不等式
不等式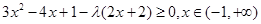
恒成立即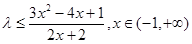 恒成立
恒成立
令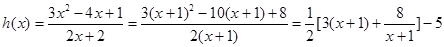
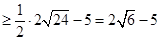 当
当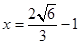 时等号成立
时等号成立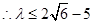

练习册系列答案
相关题目
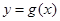 的导函数的图像与直线
的导函数的图像与直线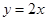 平行,且
平行,且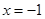 处取得极小值
处取得极小值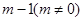 .设
.设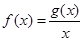 .
.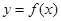 上的点
上的点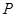 到点
到点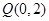 的距离的最小值为
的距离的最小值为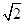 ,求
,求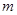 的值;
的值;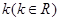 如何取值时,函数
如何取值时,函数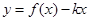 存在零点,并求出零点.
存在零点,并求出零点.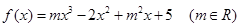 且
且 在
在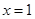 处取得极小值.
处取得极小值.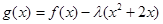 在
在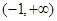 上是增函数,求实数
上是增函数,求实数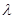 的取值范围。
的取值范围。 是定义在
是定义在 上的奇函数,且
上的奇函数,且 在
在 处取得极小值
处取得极小值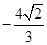 。设
。设 表示
表示 满足:
满足:
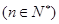
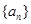 的通项公式
的通项公式 ;
;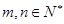 ,若
,若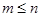 ,证明:
,证明: ;
;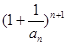 与
与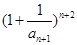 的大小。
的大小。